The Subjective Is Objective

Sentience, the central object of all ethics and of all action, is a reality of the world. It is a reality in itself; an objective reality, one that does not exist merely from some private point of view. In the same sense as a table or a stone are made of matter, our brains too are made of matter; thus, sentience is a potential property of matter in general. Its existence is a fact of physics, and it is the task of physics to give us an account of how sentience is linked to other aspects of reality and to show us how to determine when, where and with which qualities (suffering, pleasure and other qualia1) it occurs.

Despite this, present-day physics is incapable of making room for sentience in its description of the world. The problem would not be solved by discovering some new phenomenon or some new law. We need a complete overhaul of our ideas of reality and of physics. I do not have the keys to such an overhaul; I will be content here with showing why I believe it necessary, and suggest a few conditions that it will have to satisfy.

My reflections are in large part inspired by the views of the English mathematician Roger Penrose as expressed in two of his works2 in which he argues that our current physics is unable to explain mental processes. He considers specifically our capacity to understand mathematical reasoning, a capacity he says cannot be simulated by the execution of an algorithm; this limitation follows, he argues, from the well-known Gödel incompleteness theorem (1931). I believe that this reasoning is very important, but not quite conclusive. Between the lines in the works of Penrose, I see the basis of my own central argument: the inescapability of the internal, subjective point of view, and the fact that this point of view makes it impossible to build a theory of the world without attributing to the subjective, that is, to sentience, and also to the truth-value of prescriptive assertions and to the reality of freedom of choice, the status of facts. It's on this basis, I believe, that can be confirmed Penrose's conclusions, particularly his assertion that the evolution of the world cannot be entirely subject to a computable determinism. If the world is deterministic, it must be so at least partly in a non-computable way, that is, in a way that is not algorithmically reproducible.

Penrose reasons on the basis of one of the most abstract, and specifically human, forms of thinking, specifically mathematical reasoning. What his works suggest, however, is that all authentic forms of understanding – including very practical reasoning, of the kind certainly many non-human animals are capable of – necessarily comprise a non-algorithmic process. Authentic understanding implies the perception of the truth of certain facts, whether these be the approach of a predator or some mathematical truth; it cannot be reduced to the necessarily insentient execution of an algorithm. I will argue that sentience, intelligence (the faculty of understanding), freedom and ethics (the non-algorithmic search for the right answer to the question “What to do?”*) are closely connected and that consequently intelligence, freedom and ethics are properties of every sentient being.

This will give us the means to discern, or rather to better found, a number of criteria that we feel natural to resort to when we wish to determine if a given being is or isn't sentient; such as the non “automatic” nature of its behaviour or the presence of tissue of a certain kind, such as nervous tissue. It will give us indications concerning the place of sentience in evolution. It will allow us to found, as true, our moral obligations towards all sentient beings. Lastly, it will imply the necessity of reconstructing our conceptions of physical reality and will allow us to sketch some constraints that these new conceptions will have to satisfy.

1. Conflicting Certainties

My assertion that our current physics is unable to account for sentience may come as a surprise to some. Indeed, it is at odds with that of quite a few philosophers, including several antispeciesist philosophers. Peter Singer, for example, spends eight pages in Animal Liberation3 countering the Cartesian position according to which animals are insentient and feel nothing at all. Singer puts forward several arguments, all of a scientific nature, without ever mentioning a problem with the scientific status of sentience itself. His arguments concern the behaviour of animals, the presence of nervous tissue and the evolutionary relevance of pain. On the same basis, he argues against sentience in plants4. Another frequent argument is the presence in some animals of certain chemical substances, such as endorphins mentioned by Joan Dunayer in her article “Fish: Sensitivity Beyond the Captor's Grasp”5. Following my experience, antispeciesist activists quite generally tend to believe that the scientific status of pain and sentience is unproblematic and that our inability, for example, to determine whether or not an ant can suffer is only the result of a lack of attention on the part of scientists to the issue.

This attitude sharply contrasts with a view very frequently shared precisely by persons with a scientific background and who claim to speak for a certain rationalism. Their tendency is instead to declare the question of whether a given animal is sentient as meaningless. Erwin Schrödinger, one of the founders of quantum mechanics, expressed this idea – that he didn't share – very clearly, in the answer he imagines a “rationalist” would give to the question “What kind of material process is directly linked to consciousness?”6:

A rationalist may be inclined to deal curtly with this question, roughly as follows. From our own experience, and as regards the higher animals from analogy, consciousness is linked up with certain kinds of events in organized, living matter, namely, with certain nervous functions. How far back or “down” in the animal kingdom there is still some sort of consciousness, and what it may be like in its early stages, are gratuitous speculations, questions that cannot be answered and which ought to be left to idle dreamers. It is still more gratuitous to indulge in thoughts about whether perhaps other events as well, events in inorganic matter, let alone all material events, are in some way or other associated with consciousness. All this is pure fantasy, as irrefutable as it is unprovable, and thus of no value for knowledge.

Mind and Matter, ch. 1

This position, which claims to be “rationalist”7 discards as meaningless the issue of animal sentience (consciousness). It does accept, however, without qualifications, that “we” are sentient – “we” being human beings. It treats our own sentience as an empirical fact, one that is part of the reality of the world, that is furthermore linked in some way to “nervous functions”, in other words to ordinary observable physical events. But outside the human species – and a few “higher” animals – the status of sentience changes radically. For “lower” animals and inanimate objects, the claim is not that they lack sentience; rather, it is that in their case the issue of sentience is meaningless. It is no longer, in their case, in the realm of facts.

These two sides have in common that they see the issue of the scientific status of animal sentience as unproblematic: the pro-animal philosophers because they believe that it has essentially been solved; the “rationalists” because they regard it instead as meaningless. I wish to call into question these two placid certainties; and in particular, that of “my side”, of those who struggle for the respect of the interests of animals. Indeed, the opposing position, which dominates among scientists, has its reasons; and to dialogue with these scientists and with our society as a whole which trusts these scientists, and to answer their arguments with sincere and convincing counter-arguments, we must recognize these reasons. More broadly, reality belongs to us as much as to anyone; we must not allow that in the name of science, that is, in the name of reality, the existence or relevance of animal sentience be denied. We must thus understand the real difficulties there are in making room for sentience within the scientific point of view, and start looking for ways to solve them.

This question has direct practical consequences for the interests of non-human animals. Florence Burgat has described8 the tendency among researchers of the INRA (French national institute for agricultural research) in charge of the issue of animal well-being to view the object of their study as a non-issue, as a mere reflection of “social pressure”, of a fantasy of the ill-informed public opinion (ill-informed because out of lack of scientific vision laypeople take seriously the idea that animals may have authentic well-being). Their studies will consequently aim at contenting this social pressure as cheaply as possible. The well-being of animals will be measured by their health, a criterion seen instead as “objective” and itself measured in terms such as growth rates and other criteria very much in harmony with the interests of the tradesmen, these interests being for their part viewed as very real. When scientists have the mission of studying what is, and believe that animal suffering is not, or – equivalently, as they see it, that the question of animal suffering is meaningless – any serious social consideration of animal interests is impossible.

2. Humans and Stones

The central thesis of this article is twofold, both supporting and opposing each of these two certainties. It posits:

— the inescapability of the subjective point of view, and the impossibility of not believing that ethical assertions – also called prescriptions – possess a truth-value and  that sentience and free will are objectively real;

— the impossibility of integrating sentience and the above other facts into the framework of physical reality that still dominates our minds today.

These two impossibilities lead to a contradiction if one takes this conception of physical reality for granted. I will return to each at length, but I also believe that there is a hazy but widespread and persistent awareness of this clash in our culture. The two assertions are rarely articulated, and the contradiction to which they lead is rarely brought to light. Instead, we divide the world mentally into two radically dissimilar compartments: we treat it as made of humans on one side and of stones on the other. The two contradictory assertions are each viewed as true, but separately: one as true in the world of humans, the other in that of stones.

Let us take up the “rationalist” position depicted above by Schrödinger. It starts by accepting sentience as a fact in the world of humans: “According to our own experience, (...) consciousness is connected...”. Consciousness, therefore, is a reality in human beings. Since these are part of the physical world, one could imagine that the same concept of sentience would be applicable everywhere in this world; not that sentience is necessarily present everywhere, but that where it is not present, it is at least absent. But this is not what this “rationalist” position goes on to say; it tells us that beyond the limits of the human world9 the very question of sentience is a matter of “gratuitous speculation”; to such questions “no answers can be given”. Outside the human world, sentience is a concept without meaning.

Schrödinger's “rationalist” does not, however, completely deny that the laws governing the non-human world also apply to the human world; sentience, he says, is connected to certain kinds of events within matter. But he does not specify in any detail this “connection”; and if there is a connection, it is not clear why its presence or absence should not remain discernible outside the human species, including anywhere “down” the ladder of animal species. So he does not seem to be really convinced of the possibility of establishing the said connection. Others, who are less attached to their reputation as “rationalists”, will explicitly make “man” a domain ruled by different laws than those that govern mere matter; they insist that we are both body and spirit. This was the position of Descartes, who is often regarded as one of the main founders of rationalist thinking. Today, such attitudes are often less openly proclaimed, and what is displayed is a kind of schizophrenia elevated to the status of an article of faith; on the one hand, one claims to accept the laws of modern physics in their entirety, and on the other, one maintains that the human being is of another order. This is typically the religious-secular attitude; it is the one promoted by the Catholic Church, and which it still blames Galileo for not having displayed, or not enough.

The general rule is to admit in principle that the human being, including the nervous system, must surely be subject to the same laws of physics as the rest of the universe; but this statement remains vacuous, devoid of any operative power. The complexity of the nervous system serves as both a good reason and an alibi; a good reason because this complexity is real and would make it impossible to analyse in detail, particle by particle, all the events that take place in a brain; an alibi, however, because, beyond the petition of principle, one feels, confusedly or clearly, that complexity does not really make any difference, and that sentience simply cannot arise from this kind of physics which, basically, describes the world as a set of billiard balls evolving “mechanically” – that is, according to laws of computable determinism.

This division of the world between humans and stones extends to virtually all our concepts. At the heart of our legal system is the distinction between persons and things; everything that is not human is a thing, including all non-human animals. At the heart of our philosophy is the opposition between culture and nature; only humans have to do with culture and everything else belongs to nature. Our universities are systematically divided into literary disciplines on the one hand, which study the mind and the “humanities”, and the scientific disciplines on the other hand, also known as hard science (as hard as stones), which study rocks, trees and mice. Sociology and anthropology belong to the former, ethology and chemistry to the latter. A gulf exists, it is said, between humans and other animals; the former think and decide freely while the latter are driven by instinct as a stone is by gravity.

Animals: grains of sand among the stones

The radical Cartesian exclusion of all non-human animals from the realm of sentience is intimately linked to the division of the world into humans and stones, and this in turn is linked to the double impossibility mentioned above. The animal question is thus directly involved in the solving of this double impossibility.

If the world were really made up of two easily identifiable categories of objects, a sharp conceptual partition could be defensible. We could consider that some concepts apply to one category of objects but not to the other. This would be the case, in particular, for those that underpin our ethics, in their various forms. Even without a precise definition of the notions of sentience, autonomy, dignity, free will and so on, we could see that all the signs that spontaneously lead us to believe that a given human possesses one of these characteristics are satisfied by all humans and by no stones. Therefore, given any object of the world, we would need no other criterion than that of its belonging or not to the category of humans to allow us to decide whether it should be viewed as a moral patient, that is whether we should consider it for its own sake in our deliberations.

This is the world as humanism would have it, as our culture in general would have. Yet this is not how the real world is, as we know very well. Already within the human species, not everyone displays, at least clearly, the signs that I have mentioned; there are embryos and fetuses, the comatose and the profoundly mentally impaired. It is above all the moral status of embryos and fetuses that has been debated, because of the issue's practical importance and also because of the obvious continuity in the development from the fertilized egg to the newborn and beyond. If there is a chasm between things and people, it is quietly and effortlessly that the embryo seems to cross it, at some moment we are not even able to determine.

However, this gap is awkwardly contained by invoking the fact that the beings in question, even if they do not possess the features of a typical adult human, are at least destined to acquire them (in the case of embryos), or used to possess them (in the case of the comatose); or possess them by essence, though by “accident” they do not (in the case of the profoundly mentally impaired). The partition of the world into persons and things is thus saved.

It is the non-human animals who make this view untenable. Apart from human beings, there are not just stones. The world is not made up of two categories of objects that are sufficiently distinct for the problem of ethical criteria not to arise. It is not obvious that a chimpanzee is not sentient and has neither dignity nor free will. And if there is doubt concerning chimpanzees, there is doubt too in the case of cats; and in that of fish, that of octopuses, ants and jellyfish, and perhaps even plants. The coral is an animal, related to a jellyfish, but does a coral not look like a stone? Is there any doubt concerning the stones themselves? Probably not, but we would like to know why.

The animal question, by simply pointing at the existence of animals and thus to a prima facie continuity between the world of humans and that of stones, forces us to acknowledge the need for a criterion of moral patience that can be applied to any object in the world. All objects of physics are thus, at least potentially, objects of ethics; the question of their possession of this or that ethically relevant feature – and first among these, of sentience – can, for each of them, be answered positively or negatively, but is never without meaning.

Therefore, the solution that our society adopts to “solve” the double impossibility, which is to seal off the two conflicting theses from each other, each considered valid in its own domain, breaks down. These theses instead meet and collide in a common domain, that of the non-human. We cannot believe that “asking how far down the ladder of animal species there is still some form of consciousness” is a question without meaning; we will need to answer it to determine whether or not we have moral obligations to these non-human objects. This will be true even if we adopt the ethics most hostile to the consideration of non-human animals; if our criterion is not sentience but the possession of rationality, for example, we will need to be able to apply it to any object in the world, even if our intention is to show that, in fact, only humans are rational.

There then remains no point in trying to preserve the domain of the human from the indignities of physics; we must accept that there is only one world and that we are fully part of it; and that sentience, or any other characteristic that we deem relevant to ethics, is of that world, and as such belongs to physics. We must recognize that ethics and physics have the same field of study, the same world. Ethics cares about the humblest pebble, at least in the sense that its criteria must be able to tell us whether and why we should care about it or not.

The criteria of ethics must apply to all objects of the physical world, and it is only by physical means that we can determine whether or not these objects satisfy these criteria. If our criterion is sentience, we can only determine whether an object is sentient by observing it. And we know that everything we observe – the movements, sounds and so on it may make – are physical occurrences, and are related, through the laws of physics, to processes taking place in the object. If we believe that these observed occurrences are indications of the object's sentience, while they are caused by physical processes taking place in the object, sentience itself must be a physical phenomenon. The same reasoning applies to any other ethical criterion one might wish to adopt.

The ongoing crisis of physics

It follows that we have no way out of the double impossibility without altering our conceptions of physics. In the following sections, after examining in more detail the first impossibility, namely the inescapability of the subjective point of view and the impossibility of not believing certain things, I will turn to the reasons for the second impossibility, that of incorporating sentience and other subjective features into the dominant view of physics. One might answer: very well, but modern physics is all but unassailable, and cannot be subverted just because of the ethical problem of the moral status of animals. I recognise the strength of modern physics. However, I also know that it is in deep crisis and that it has lost its foundations. The solidity that is generally attributed to it is largely due to its practical accomplishments, to the impressive power that it gives us to master matter; but also to its alleged capacity to provide a consistent and intelligible view of the world. However, it has lost this capacity since the advent of quantum mechanics in the 1920s. The previous picture, now obsolete, of the way physics described reality has nevertheless remained dominant by default, as a picture of ideal physics, both in the minds of the general public and in those of a vast majority of scientists, even those who are familiar with quantum mechanics. It has remained so precisely because quantum mechanics has given us no credible alternative vision.

I believe, however, that this classical ideal of a computable, billiard-ball determinism is itself inconsistent and ultimately indefensible; this is because it is incompatible with sentience, but also because, if its logic is carried to its conclusion, it self-dissolves into a purely mathematical construct devoid of substance. Therefore, we should not hope to solve the crisis of modern, quantum physics by returning to the previous paradigm, as physicists such as Einstein dreamed of doing in the early days of quantum mechanics. Rather, we must draw on the “quirks” of quantum mechanics, and on the constraints that follow from the reality of sentience, to try to imagine what an alternative worldview might be.

I will explicit later (section 5) the elements of the structure of this pre-quantum physics that serve my argument. I will not attempt to paint a picture of quantum mechanics, however, and will only refer where useful to some of its features. There are good introductory books on quantum mechanics on the market that give an idea of the strange structure of this theory, the most orthodox interpretation of which denies the existence of an objective reality10.

The cry of the carrot

If taking the animal question and the issue of sentience seriously has profound implications for our physical conceptions, I believe that conversely a reflection on physics, and at least an awareness of the inadequacy and inconsistency of our traditional conceptions of physical reality, can allow us to move beyond empty debates and start providing valid responses to some of the objections that we, as animal activists, receive. One example of such an objection is the infamous “cry of the carrot”. Beyond the obvious bad faith behind it, this objection expresses almost explicitly the unease that derives from the impossibility of integrating sentience into our vision of the physical world. We do not get the answer “What about the cry of the carrot?” if we argue in favour of oppressed Chechens; these are humans, and so the question of what physical criterion justifies ethical consideration for them is not asked. But if we care for non-humans, even for some as close to us as pigs or cows, we implicitly show that we do not believe in the partition between humans and stones; our criteria must then necessarily be physical. We are thus referred to a physical phenomenon – the squeaking sound of a carrot being grated – and are asked how we can distinguish it from a cry, from a real expression of suffering, since we do not limit this notion of suffering to the human world alone, but view it as part of the physical world, the one that includes pigs, carrots and stones.

We can already answer, of course, that carrots have no nervous systems and so on. But we have to admit that we don't know why these criteria are not arbitrary. What is it about nerve tissue that makes it the unique site of potential suffering? What we lack is a theory of suffering, and a global vision of the physical world that makes this theory possible. From then on, we will be able to tell from the outside whether or not this or that phenomenon that we observe – a certain sound, for example – corresponds to suffering, without needing to be “in the shoes” of the carrot any more than we need to be in the shoes of an electron to determine its state.

3. The Argument by the Impossibility of Nonbelief**

One may distinguish three kinds of “reasons to believe” the truth of an assertion:

A. Demonstrative reasons (facts and reasoning that make the assertion probable, such as believing that tomorrow it will rain because the weatherperson says so and is rarely wrong).

B. Ethical reasons (in particular, for the utilitarian, it is right to believe something if doing so will increase the total happiness in the world).

C. Causal reasons (any cause of which the belief is an effect; such as the fact that most people believe in a certain religious creed because their parents and relatives believed in it).

It may seem odd to view a purpose as a reason for believing something (reasons of type B). However, for acts in general, a purpose is usually viewed as a valid reason.

One may think that the ideal reasoning in favour of a thesis must be of type A, the model of which is perhaps mathematical reasoning. In such cases, one does not appeal to the advantages for the reader of believing in the truth of an assertion (which would make it an ethical argumentation, type B) and one does not try for example to hypnotise the reader into believing in this truth (an “argument” of type C). Whether the reader likes or not that in a right triangle the square of the hypotenuse is equal to the sum of the squares of the other two sides, that is what he or she is shown.

Only type A reasons for belief can be a valid answer to a question of type “Why do you believe...?” An answer of type B, that is, “I believe it because it is better for me (or for others)”, cannot replace a reason of type A11. Nor can I answer that I believe the assertion because of my upbringing, or because my neurons are configured in such and such a way (answer of type C). Such answers may well actually be true but are not answers to the question as asked.

My wish is to show that ethical (i.e. prescriptive) assertions have an objective truth-value, and thereby to show in particular the objective reality of sentience and of free will. I would be happy if I could base these developments solely on type A reasons. But I cannot.

Shall I then turn to a type B argument, and simply make you desire to believe what I enjoy believing? Or find a way to persuade you by rhetorical tricks that my ideas are correct (give you a type C “reason to believe”)? That is not my intention. I believe that I am justified in using yet another form of “argument” in this case. It does not consist in giving a reason to believe, but in highlighting the fact that we already actually do believe, and can but believe12. Henceforth, acknowledging this fact is only a matter of consistency.

One may find such an argument weak since it is not a demonstration. My response is partly ad hominem, but not, I think, without force. It consists in noting that it is this same form of argument that ultimately underpins everything we believe, starting with our conviction that there exists a world.

This last fact is actually universally recognised; I will get back to this in a moment. What is remarkable is that while being recognised it is generally ignored, the impossibility of basing our belief in a real world on pure reasoning being perceived as a sort of philosophical curiosity that detracts nothing from the good standing of this conviction; whereas the corresponding impossibility in the ethical domain – the impossibility of basing the truth of ethical propositions on pure reasoning – passes for irrefutable proof of the relative or conventional character of these, or, in the views of religious people, of the need to base them on faith in a god.

On the contrary, I think that the truth of ethical (prescriptive) assertions is as well-founded as that of those assertions classically called “descriptive” such as those that describe material realities13. Both are based on the same impossibility of nonbelieving certain assertions despite the impossibility of proving them. If my argument is to be considered weak, it cannot be more so than our belief in the existence of the world; which should be enough for almost any purpose.

Before we discard this argument as too weak, we should grasp its full meaning. The impossibility of not believing that grounds it is not a mere difficulty; it does not refer, for example, to the psychological suffering that nonbelief would cause. It refers instead to an impossibility that is inherent to our way of being in the world. Let us consider that, because of our very presence in the world, because of our situation as sentient beings, it may be impossible for us not to believe something. It is then futile to pretend not to believe it. Any theory we build that contradicts this belief would be impossible to take as true without believing both one thing and its opposite; that is, it would be impossible to take seriously as true, once we become aware of its implications for our inescapable belief. This does not, of course, preclude us from speculating, imagining false what we cannot believe to be false; we may perhaps draw interesting conclusions from such speculations, but cannot believe the world thus contrived to be real.

I now come to the substance of my argument; my first step will be to highlight the impossibility of our nonbelief in the reality of the truth-value of ethical (that is, prescriptive) assertions.

4. Ethics

The impossibility of universal nonbelief

We often know clearly whether or not we believe something. I believe that this is now Saturday, and I know that I believe it. But sometimes it is not so easy. A good example is the question of faith in Christianity, which is central to that religion since the necessary and sufficient condition for being “saved” is to believe in Jesus (in his existence, his divinity, his resurrection, etc.). Hence the nagging concern for every Christian: “Do I really believe?” The simple statement – the “profession of faith” – is not enough. The story of Jesus walking on water and of Peter sinking because his belief that he could do the same was not strong enough shows well that we do not always know whether we believe something or not, or to what extent we believe it; for Peter rises, believing that he believes, but not believing enough; he sinks, and Jesus, somewhat perversely, asks him: “O thou of little faith, wherefore didst thou doubt?”14.

In this story, sinking or not sinking represents a supernatural test of belief. A more mundane test is this: if we believe something, it will be reflected in our decisions.

Do we believe in the existence of a physical world? I don't mean whether we believe in the complete validity of some specific physical theory; I mean, in a minimal sense. For example, do I believe in the existence of the keyboard in front of me? The answer must be yes; the fact that I am typing on the keys to write this text is explained by my belief that this action will change something in the world. I may not know very well what the world is, what matter is, and what it means for it to be changed. But I do know one thing: that it will change something for sentient beings. If I type on the keys, tomorrow I will be able to read what I will have written; and perhaps others will read it too. I believe in the existence of the world at least as a basis for a causal chain such that depending on how I act, sentient beings – myself, at least – will be affected.

The fact that I type on this keyboard thus testifies to my belief in the existence of the world, at least in this minimal sense of “existing”.

This, one may say, is trivial. But it means that we are many to believe in the existence of the world! All sentient beings do so, as I see it; but for the moment we will accept that this belief seems plausible at least for all typical adult human beings – for the non-comatose, for example. They eat and hence believe in the existence of what they see on their plates, or at least in the fact that in some way the movements they perform will cause or remove some sensation of pleasure or of hunger.

An unimpressive result, perhaps, but one that contradicts a tradition that goes back at least as far as the Greek sceptic Pyrrho (4th-3rd century BC), who claimed to doubt the very existence of this world. According to Diogenes Laërtius, Pyrrho believed so little in the testimony of his senses that he only avoided falling off cliffs thanks to the actions of his friends***. This is a rare case; yet, if this account may testify to Pyrrho's nonbelief in the existence of those cliffs (leaving aside doubts about what he would have done in the absence of his friends), it does not imply his nonbelief in the world in general. Quite the opposite: for why then did he put one foot ahead of the other, if not to move forward, or at least to relieve the urge to move – which by itself implies a belief in some effect, never quite immediate, of his actions?

In fact, Descartes, taking up this same question of the ultimate foundation of our beliefs in the existence of the world, began by “doubting” everything; but this doubt was only provisional, heuristic, and did not imply practical consequences15:

(...) so that I might not remain irresolute in my actions, while my reason compelled me to suspend my judgement, and that I might not be prevented from living thenceforward in the greatest possible felicity, I formed a provisory code of morals, composed of three or four maxims (...).

These “three or four maxims” are practical and imbued with solid common sense. They aim, as Descartes says, at felicity (happiness), that is, at a sensation. Descartes derives action from belief (“judgement”) since he fears that in the absence of any belief he will remain “irresolute in [his] actions, while [his] reason compelled [him] to suspend [his] judgement”; yet he claims to be able to compensate for this lack of belief by a “provisory” (provisional) morality. It seems clear, however, that this morality itself necessarily presupposes a belief. The first maxim, for example, “was to obey the laws and customs of my country”; he, therefore, believed in the existence of that country. Descartes thus never really ceased to believe in the reality of the world; he was never irresolute in his judgements on this point. His doubt, which was provisional, was only about their foundations.

By these examples, I want to suggest that the existence of scepticism, philosophical or otherwise, concerning the existence of the world does not imply the existence of any real doubt on this subject. This is not to say that these people are faking it. Descartes himself did not really claim to have doubted the existence of the world. Others may have sincerely believed they had such a doubt, but that doesn't imply that they really had it16.

But my point is not simply to note that particular persons did not really doubt everything, or even to assert that no one ever really entertained such a doubt; it is to show that such a doubt is impossible, because of our situation – because of the situation of every deliberative being, and therefore, I believe, of every sentient being.

Our situation is that we must, at every moment, decide. It is not that it is in our interest to decide; it is that it is impossible for us not to decide.

Let us imagine that we do not believe anything. Then we do not believe that our action will have any particular effect. Why then should we bother to act? We could just as well do nothing. But why do nothing? To avoid getting tired? If we do not believe anything, we do not believe that acting will tire us, nor that doing nothing will tire us less.

Nor can we decide without reasons. When we are irresolute, we look for a reason to decide one way or the other; only with such a reason can we decide. Yet, as long as we remain irresolute, we have at least decided one thing – namely, to decide nothing else. We could run around, or take some other decision; if we don't, it is because we have a reason not to, if only, for example, not to tire ourselves unnecessarily. Descartes, in order not to “remain irresolute”, adopts a moral system, that is a system of reasons for deciding one way or the other; but he does not choose just any moral system. When he states his “three or four maxims” he also justifies them. He does so based on practical, “reasonable” reasons, which he believes in, despite the “doubt” imposed on him by reason.

Descartes, therefore, believes in reasons for deciding, in the “factual” sense; that is, he believes in the existence of a certain country, namely, the one in which he lives, in the existence of its laws and customs and so on. But he also believes in these reasons in the prescriptive sense: he believes that these are reasons to decide to act in a certain way. He believes in the existence of prescriptive reasons.

In short:

— it is at every moment impossible for us not to take decisions;

— we cannot take decisions without believing in reasons for doing so (prescriptive reasons);

— it is therefore impossible for us not to believe in reasons for taking decisions (prescriptive reasons).

Inside and outside viewpoints

It is worth emphasising here the position from which this conclusion is reached. This is what I call the “inside viewpoint”. One could imagine describing the same events – a person deliberating, then deciding and acting – from an outer point of view, as a physical system going through a sequence of states according to certain laws. Perhaps we will then identify some of these states as certain beliefs; and find that the system always happens to be in a state of belief in one thing or another, and that this state determines the system's subsequent evolution, and in particular determines its future actions. No doubt will we also try to explain this state of belief by the laws of motion of atoms, or, at another level, by Darwinian mechanisms of evolution. This outside point of view is valid in its principle, since we are part of the world, and are therefore physical systems; such descriptions and explanations are necessarily possible. Nonetheless, however legitimate it may be, this outside viewpoint cannot abolish the inside viewpoint. The outside viewpoint observes and explains our belief; but the observation and explanation of our belief are not our belief, and do not, by their mere existence, abolish our belief.

However, it may happen that how we observe and explain one of our beliefs constitutes a reason to cease believing it; for example, when we explain an optical illusion. We may then abandon the belief. But it may also be that this is not the case and that we do not abandon the belief, perhaps because we have not been convinced by the explanation, or because it does not really seem to contradict the belief, or for any other reason; whatever the reason, it is vain to attempt to persuade ourselves that we do not believe, as long as we do believe. And this will always be the situation concerning certain beliefs, if, as I hold, it is impossible for us not to have them because of our condition as deliberative beings.

A criticism often levelled at scientific descriptions and explanations of subjective phenomena is that of “reductionism”. I view this criticism as, in its substance, correct; not that we should refrain from describing these phenomena in scientific terms, nor that we should attempt to add, as is so often done, some holistic layer of “emergent phenomena” based on the questionable principle that the whole is more than the parts. Rather, I believe that these descriptions and explanations are themselves made in the terms of a physics that is incompatible with subjective phenomena, and that to accept them would be to accept that this outside point of view could abolish the inside one. But this abolition, as I have said, is not possible. A physics that has implications we cannot believe is itself a physics we cannot believe.

The reality of the truth-value of prescriptive assertions

Foremost among those things that we cannot nonbelieve is the existence of reasons for making decisions, that is, the existence of the right (correct) answer to the question “What to do?”. The answers (right or wrong) to this question are not descriptive assertions, in the classical sense, but instead prescriptive. They are of the form “Do this!”. They are not to be confused with simple predictions, such as “I will do this.”.

One may find this new category of assertions mysterious. What is their truth-value? In what sense can the proposition “Do this!” be true? First of all, such a proposition does have a negative: “Do not do this!”. Secondly, belief does not in itself constitute the truth of such propositions; we can be wrong. After having thought “Do this!”, we may change our mind: “No, instead, do this other thing!”. We may also reconsider afterwards: “I should not have done that.”. If belief in the assertion was its truth, we could not change our minds, that is, feel that we were wrong. The act of deliberation itself would be meaningless – any conclusion we reached would be right, by the mere fact that we reached it. It would be like looking in a meadow for the blade of grass that we will have found in it.

If the truth-value of prescriptive assertions is not defined by our belief in their truth, then it exists independently of this belief. To search for the right answer to “What to do?” necessarily assumes that a certain answer is the right one, whether we find it or not. It would make no sense to search for it if we did not believe this; but it is impossible for us not to search for it, and it is therefore impossible for us to nonbelieve that a certain answer is right, regardless of our perception of its being right. It is in this sense that we cannot nonbelieve in the reality of the truth-value of prescriptive assertions.

Ends and means

We should not view deliberation as a purely factual search, such as “Given that I have a certain end, what is the best way to achieve it?”. If this were the case, what I call a “prescriptive assertion” would be no more than a descriptive assertion, in the usual sense: “Given that I have a certain end, here is the best way to achieve it”. But we also choose our ends. Even a completely “selfish” person has chosen to consider only her interests, excluding those of others. This implies at least her belief in the factuality of the possible future satisfaction of her interests, that is, if she conceives her interests in terms of obtaining pleasure and avoiding suffering, that she believes in the reality of her future pleasure and suffering17. She cannot believe that things that do not exist in reality are an end for her. But she will also have to believe that this future pleasure and suffering can be the result of her actions; she will therefore have to believe in the existence of a physical world, at least in this minimal sense. Finally, the satisfaction of her own interests will represent in many cases not one, but several at least partially conflicting ends; she will have to choose between qualitatively different pleasures, between pleasures in the near future and others more remote, to decide whether a certain pleasure is worth the suffering needed to obtain it...

It is also possible to imagine that an individual may view his “interests” in terms other than pleasure and suffering. One example is the idea (based on a misinterpretation of Darwinism) that our “real” interests are the propagation of our genes. Another results from a certain romantic individualism, for which our interests consist in something like “self-realisation”18. If some people do take such ends seriously, this only confirms the plurality of our possible ends, and thus the fact that these, like our means, are the result of a choice.

I believe that in reality this distinction between the choice of ends and that of means is artificial. In our real deliberations, both are intertwined. No doubt the temptation to posit such a distinction and to seek to eliminate the choice of ends by taking them as constants stems from our difficulty in conceiving on what basis this choice could be made, if we view it as free. I will return to the problem of free will. For the moment, let us just remark that the choice of means, once the ends are determined, is not necessarily less problematic in its mechanism. The solutions that a sentient being finds to achieve a given end are often “innovative”, and the hypotheses put forward by Penrose suggest that our brains allow for modes of problem-solving that could not be simulated by an algorithm, and are therefore not deterministic in the sense of computable determinism.

A meaning “for me”?

We cannot refrain from deciding, and cannot decide without asking ourselves “What to do?”; and we can only ask this question, like any question, if we believe it has a meaning.

We cannot say, “Yes, I give this question a meaning, but that is because I cannot do otherwise; but I do not believe that it really has a meaning”. If we don't believe it really has a meaning, we don't believe it has a meaning at all.

Nor can we say, “Yes, it has a meaning, but only for me”. This process of relativisation is often used also concerning “descriptive” statements in the classical sense. I think it is worth examining what it asserts.

“For me” may mean “this is what I believe”; then “x has a meaning for me” signifies “I believe that x has a meaning (but others, perhaps, do not)”. The assertion that x has a meaning is then not itself relative, but instead absolute. I can say, “For me the earth is flat”; the flatness of the earth remains an absolute question because it is true or false that the Earth is flat, independently of me. To say that prescriptive assertions make sense to a certain individual is then to say that this individual believes that they make absolute sense. This then grants my point: we all believe that prescriptive assertions have a meaning.

In other cases, the expression “for me” denotes a different kind of relationship between the statement and an individual. An apple may taste sweet to Anne, and sour to Valerie; its “objective taste” does not exist. This does not mean, however, that the taste it has objectively for Anne does not exist, as does the taste it has for Valerie! In this case, we could say that the having-a-meaning of x is an objective truth, but in relation to me. This relation could be the simple fact that it is indeed I who believe that x has a meaning; we are then back to the first interpretation of “for me”. The relation could also be the fact that the prescriptive assertion x is itself related to the entity “me” (if we accept the existence of such a “personal identity”19): it prescribes what I should do. It is a truth about me, in that sense; but a truth I believe in, just as I believe (or not) in the flatness of the Earth.

It is remarkable that this relativisation – this “true for me” – works as if “me” were an entity somehow beyond the world, and could as such somehow bring the very truth in question with it into its retreat. Given that we are part of the world, our very view of the world is part of the world. If we believe that prescriptive assertions have a meaning “for us”, we believe that they have a meaning, period.

Ethics as a theory of the correct answer to the question “What to do?”

I have so far discussed prescriptive assertions; I think we can also call them ethical assertions. More precisely, I believe that a prescriptive assertion – the assertion “Do this!” – is true if what it commands us to do is what ethics commands us to do; and that therefore deliberation – the pondering of the question “What to do?” – is the search for the ethically right action.

I do not say this in a normative sense; that is, that all deliberation should be the search for the ethically right action. I am saying that in fact it is such. I propose to define ethics as the theory of the right (true, correct) answer to the question “What to do?”.

I will be told that I am free to define words as I wish, but that my “ethics” is not ethics in the ordinary sense of the word. I do not believe that this objection is justified. More specifically, I believe that my definition of ethics follows from the common usage of the term if only one ceases to make an arbitrary exception regarding decisions that concern only oneself, and accepts the absolute truth of prescriptive assertions.

Selfish and ethical behaviour are usually contrasted. The point of ethics, it is said, is to lead us to consider others and respect their rights and interests, instead of paying attention only to ourselves. Some ethical conceptions make this restriction explicit. Contract theories, for example, essentially require us to respect the terms of our “contract” with others, but concerning ourselves we are “free” to do “as we please”20. At least one ethical theory, however, governs in principle all our choices, placing on an equal footing those that concern ourselves and those that concern others: for hedonistic utilitarianism, we must act to maximise net happiness in the world; therefore, an act that increases our own happiness without affecting that of others is ethically obligatory, just as is an act that increases the happiness of others.

This fact is rarely perceived, perhaps simply because there is little need to order people to pursue their own happiness. Yet such a command is still ethical in nature, even though we usually abide by it without the aid of an elaborate ethical theory. The same is true of many propositions in physics; we do not need to study fluid mechanics before drinking a glass of water. Physics would nonetheless be artificially mutilated if we removed from its domain what happens when we drink a glass of water; just as it is an artificial mutilation of ethics to remove from its domain “trivial” prescriptions such as those commanding us to consider our own interests.

Among the commonly mentioned ethical theories, there is at least one other that gives us obligations in choices that concern only ourselves21. This is the so-called “egoistic ethic”, whose single command is: “Maximise your own happiness!”. The fact that it is frequently mentioned as an ethic, even only as a “textbook case”, shows that common use does not exclude, at least in principle, decisions that concern only ourselves from the scope of ethics. This egoistic ethic, like hedonistic utilitarianism, governs in principle all our choices.

However, the basic reason why I say that ethics should be defined as the general theory of the true answer to “What to do?” is that all deliberation is fundamentally altruistic. Even if I am thinking only of “myself”, I am necessarily thinking of a future “myself”. My actions cannot determine the pleasure or suffering I experience at the time I choose them; they will necessarily determine my future pleasure or suffering. We are used to taking for granted our concern for ourselves. The fundamental difficulty we have in justifying ethics is often expressed by the question “Why should I rationally care about others?”, and many feel there is no possible answer. Rarely do we ask ourselves “Why should I rationally care about the feelings I will experience in five minutes?” We can just as easily say that these future feelings are completely indifferent to us! We are rarely totally indifferent to how we will feel in five minutes, just as we are rarely completely indifferent to the fate of people close to us; on the other hand, we are often rather indifferent to how we will feel in thirty years. If this were not the case, tobacco sales would suffer greatly.

Therefore, the idea that there is a radical difference between a concern for one's own – necessarily future – interests and a concern for the interests of others appears as a dogmatic and artificial construct, with little justification in either theory or practice. It is in this sense that I believe that all deliberation is altruistic; the interests it takes into account are always those of an “other”, whether that other is another individual or our future self.

“I find this hard to believe”

There remains an objection to this conception of ethics: our decisions are not, in fact, always ethical, even by the ethical standard that we do recognise. It is perfectly possible to say “I see what I should do, but I cannot bring myself to do it”22.

I believe, however, that this objection can be answered if we regard prescriptive assertions as possessing a truth-value, whether or not we know this value. It is not our verbal assent to a prescription that makes it true; nor is it the fact that we believe we assent to it.

It may be useful to draw a parallel with assertions that are descriptive in the classical sense. When a would-be parachutist finds himself unable to jump from an aeroplane, is it not because he cannot entirely convince himself that doing so is safe? He may well insist that he knows it is safe, and rehash a hundred times the facts that prove it is safe. But somewhere inside him the belief remains that there is danger. It seems to me that this implies, at the very least, that we are not quite “individuals”, in the sense of being indivisible. Consciousness is not an illusion (in whose eyes would it be one?), but its unity may well be illusory, at least in part. Hence the fact that one part of our consciousness is convinced of a fact does not prevent other parts from believing the contrary.

We often know without knowing. “I can't believe it” is often said of the death of a loved one. We may act as if he were still here; we may set the table for him, “out of distraction” – or rather, because a part of us still does not believe in his death.

To return to prescriptive assertions: we may well know that what we are about to do is not what we should do; because, for example, it will cause others more suffering than it will bring us pleasure. But we know this without fully knowing it; just as we know, for example, that the pleasure of smoking a cigarette may cause us much suffering in thirty years while still finding it hard to believe. In this light, it is because part of us does not really believe what we think we believe that we act in contradiction with our stated beliefs; and this is true whether the issue is descriptive (in the classical sense) or prescriptive.

A few months ago I climbed to the top of one of the towers of the Basilica of Fourvière in Lyon. This tower, which is open to visitors, has been climbed by hundreds of people every day for ages; I knew that it was not going to collapse just because I put one foot wrong! Everything told me that I was safe. Yet I felt dizzy as I climbed the steps; I was filled with the dread that they would break under my weight. I climbed slowly and reached the top with clenched teeth. My fear was undoubtedly irrational, but it was nonetheless real; it reflected a real belief in me that I was in danger.

I see no difficulty in viewing the problem of our non-compliance to our own ethical beliefs in the same way. We simply believe them only in part.

Description and prescription

My thesis is that we believe in prescriptions as we believe in descriptions; we believe that their content is true (or false). I also speak of their “objective truth” and their “reality”. A famous assertion – the origin of which I cannot find, and which I quote from memory – was in substance that nowhere in the universe is there anything that would resemble a prescription; and that prescriptions, therefore, do not exist as such. Moral duties, right and wrong, would only reflect our personal, “subjective”, preferences, cultural or otherwise. There would be no such thing as real ethics.

I admit that neither can I clearly define in what sense ethical prescriptions are real objects. However, I believe that the generally accepted idea that “material” objects exist is equally problematic. The verb “to exist” seems transparent, but transparency is like opacity in that it shows no content. In fact, in modern, quantum physics, the issue of the very existence of an objective reality has become highly opaque; the “standard” (so-called “Copenhagen”) interpretation is that this issue is itself meaningless. Physics is a mere set of “recipes” for predicting future observations from past ones. Everything else is no more than “gratuitous speculation”23. Paradoxically, according to this interpretation, utility (for humans), that is, a subjective, indeed, prescriptive entity, is all that is left – physical reality has disappeared, bringing with it the reality of non-human animals.

Classical, pre-quantum mechanics, which I term “Laplacian”, would appear to impart a greater consistency to physical reality. This vision remains today, as noted above, a kind of ideal model of physics, including for many scientific minds who are eager to believe in a cold and hard reality. Therefore few perceive to what extent the very logic of Laplacian physics itself leads to a dissolution of the notion of reality. I will devote the next section to a brief description of this Laplacian worldview and will highlight some of its weaknesses.

In any case, I would like us to suspend somewhat our habitual certainties according to which, to be “real”, a “thing” must be made of matter and be located “somewhere in the universe”. We are not sure what it really means for a stone to be real. Nor are we sure in what sense mathematical truths exist. Nor can I say precisely in what sense prescriptive assertions exist. I only know that neither stones, mathematical truths, nor ethical truths can be entirely taken out of existence. I believe that these things exist in the world, and therefore exist there objectively, are real. I will not make sharp distinctions between these notions, because I do not believe in those that are commonly made.

In particular, I think that if a prescriptive assertion, of the form “Do this!”, is true, then it describes a part of reality. The descriptive and the prescriptive are classically opposed; it is better to view instead every assertion as descriptive. This is why I also speak of descriptive assertions “in the classical sense” for those that are usually considered as such (the mass of a stone, for example).

Animals as moral agents

Anti-speciesist moral theories commonly distinguish between the twin notions of a moral agent and a moral patient. Humans are typically both moral agents, which means that they can (and should) act ethically, and moral patients, meaning that they should be taken into consideration when ethical decisions that concern them are made (their interests should count, and/or their rights or dignity should be respected...). Non-human animals, on the other hand, are generally only viewed as moral patients: we are to care about them, equally as for humans, but they have no duties, because they are incapable of ethical reasoning, just as are young human children, for example.

If instead, one accepts, as I propose, that all deliberation is by definition an ethical activity, and that there is no difference in nature between the deliberating individual's consideration for his own (future) interests and for the interests of other beings, then it appears that every animal who deliberates is a moral agent, in the same sense as the term can be applied to a human.

This does not mean that there are no distinctions to be made concerning the level of complexity and abstraction that an individual can reach in her ethical reasoning. The same applies to ethics as to physics. Deliberating animals are also necessarily physicists; they foresee consequences of their actions. Only a few among them, namely some humans, can build complex and abstract physical and/or ethical theories; much more often, the ethical and physical horizon is more limited; it comprises what is perceived, the near future, proximate interests and the interests of one's family or group. This limited ethics and physics is nonetheless an ethics and physics.

When we scream in fear and pain, we are saying: “This is bad!”. The scream of a pig being slaughtered says the same thing: that what is happening is bad. The anti-speciesist says the same thing: that the slaughtering of the pig is bad and says it for the same reason for which the pig says it. This same assertion, from whomever it comes, has the same meaning and the same nature: it is an ethical assertion.

If we are to believe the words that the vegetarian writer J.M. Coetzee puts into the mouth of one of his characters24, it was in part the ethics of a hen that led to the abolition of the death penalty in France:

As for animals being too dumb and stupid to speak for themselves, consider the following sequence of events. When Albert Camus was a young boy in Algeria, his grandmother told him to bring her one of the hens from the cage in their backyard. He obeyed, then watched her cut off its head with a kitchen knife, catching its blood in a bowl so that the floor would not be dirtied.

The death-cry of that hen imprinted itself on the boy’s memory so hauntingly that in 1958 he wrote an impassioned attack on the guillotine. As a result, in part, of that polemic, capital punishment was abolished in France. Who is to say, then, that the hen did not speak?

5. The Laplacian model of reality

What I call the classical, or Laplacian, model of reality emerged in the 17th century with Galileo and Newton, replacing Aristotle's physics which was dominated by finalist, animistic ideas about the nature and desires of bodies. The Laplacian model formed the basis of scientific rationalism and dominated the scientific worldview until the early 20th century. Einstein's theory of relativity (1905, 1915) still fits into this framework, which was only subverted in the 1920s when quantum mechanics made it untenable, without however providing any alternative view of physical reality.

I hope it will be clear from the short analysis I will propose of the Laplacian model that it is the paradigm that we “spontaneously” tend to view as the model of scientific description. When we insist, for example, on rejecting the notion of free will because our choices must be determined by something, this requirement is evident neither in the Aristotelian framework nor in that of quantum mechanics, which implies that certain events do indeed occur without reason. I do not believe however that the model, or rather non-model, that quantum mechanics proposes gives us a satisfactory account of free will; my purpose here is to shake some of our certainties concerning the validity of the Laplacian model. I will also show that this model does not itself live up to its own requirement that everything should happen for a reason.

I name this model “Laplacian” in reference to the striking formulation that the physicist Pierre Simon de Laplace (1749-1827) gave of the notion of determinism25:

An intelligence which, for a given moment, would know all the forces with which nature is animated and the respective situations of the beings that compose it, if moreover it were vast enough to submit these data to analysis, would embrace in the same formula the movements of the largest bodies in the universe and those of the lightest atom: nothing would be uncertain for it, and the future, like the past, would be present to its eyes.

In this view, reality – all that exists – consists of a finite or infinite collection of objects – the “beings” mentioned above by Laplace – each of which can be characterised by a number of properties that may vary over time; knowledge at a given moment of the list of these objects and their properties constitutes a complete description of reality at that moment.

A simplified view that I will often use is that of billiard balls. In an ideal billiard game, the balls move at all times according to a well-defined and computable law. As long as they do not meet a wall or another ball, they move in a straight line at a constant speed; when they collide, they bounce back elastically, following a simple law that brings into play their intrinsic characteristics (mass, radius), their motions and positions. The evolution of the whole can be complex if a large number of balls are involved, but always remains entirely predictable, at least in theory, by an “intelligence”, as Laplace calls it, informed of the laws of motion as well as of the mass and the situation (position, speed) of each ball. The “billiard ball” image of the world assumes that the whole world is a vast collection of such balls moving in three-dimensional space.

Of course, classical physics has never seriously proposed such a simplistic model of reality. The “billiard balls” picture remains relevant, however, because it captures the basic logic of classical physics, with a few subtleties. In classical physics, in the place of balls, we have “material points” – dimensionless “atoms” or “particles” that possess, for example, mass and charge – and attractive and repulsive forces of a more complex form than the simple contact repulsion that makes balls bounce. To these material points were later added fields, such as the electric field, that are distributed throughout space, mediating the forces between particles but also evolving according to their own laws. It followed that the complete knowledge of which Laplace spoke also includes that of the fields, and therefore an infinity of variables, since it is necessary to know the intensity of the fields at each point of space26. Despite this, the “billiard ball” model has all the features that I will discuss of the Laplacian model. If subjectivity cannot find its place in a “billiard ball” model, it cannot find its place in Laplacian physics27. I will often speak as if Laplacian physics were only about billiard balls because this is a simple image that allows us to highlight its workings and limitations.

It should be noted that classical physics never really succeeded in proposing a consistent and plausible theory of reality; there were always details that could not be ironed out28. The Laplacian image nevertheless remains as a paradigm for any physics that claims to be objective and allows for an observer-independent reality, because quantum mechanics proves incapable of providing such a model.

The completeness of the Laplacian model

Completeness means that all that can be said about the world is deemed to be contained in the “respective situations of the beings that compose it”; that is, to use our billiard balls image, in the position and speed of each ball.

In particular, the movements of our hands, our thoughts, our feelings, all of this would be the “mechanical” colliding of these balls according to the laws of motion that govern them. To say that I perceive the world is only to say that some of these balls, those of the world outside my body, collide in a certain way with the balls of my body, creating movements that will, in passing from one set of balls to another, end up provoking certain movements and dispositions of balls in my brain or elsewhere, movements and dispositions which will of necessity, in some way or another, constitute my perception. My feelings and emotions will in the same way be dispositions and movements of balls somewhere in me. When I act on my perceptions and feelings, for instance when I write down my thoughts on a sheet of paper, it will be because these dispositions and movements will have in turn, still following the same “mechanical” laws of motion, provoked certain movements in yet other sets of balls, which I call my hands, which will produce the writing on the paper.

Because of this completeness, the balls themselves have no “interiority”. The expression “billiard balls” is misleading in this respect. The physics of real billiard balls moving on a table describes some of their characteristics, such as their position and speed, but these parameters are relative to objects that exist independently of them and have many other characteristics that give them existence: colour, roughness, chemical composition, solidity... On the other hand, in the Laplacian “billiard ball” model, the balls have no colour or roughness; they are not made of “something”. All that can be said about them is a small collection of numbers, namely their mass, radius, position and speed. The “radius” itself is not the boundary between a full interior and an empty exterior, but a simple parameter determining if and when a “collision” with another ball will occur. This “collision” will be a change in the movement of the “centre”; but what is this centre the centre of? The answer can only be: of nothing. It is but a moving point in space. Its only existence is through its determining “collisions”, that is, events affecting other “balls”, which are themselves no more than points of the same kind. Yet all of space is points; what is special about these particular ones? There can be nothing, outside of the fact that their positions are those described by this particular collection of numbers...

If there were ever anything else to be said of this reality, if the “balls” possessed a reality beyond these few numbers, this additional reality would be unknowable to us; for our knowing it would be the same thing as particular positions and movements of certain balls in our brains, and, under the deterministic laws of movement, these positions and movements are entirely determined by those of all the other balls, and therefore cannot depend in any way on this additional reality.

As previously mentioned, the real picture proposed by Laplacian physics, based on particles and fields, is much more complex than the “billiard ball” model. The absence of interiority remains, however; the world has no “substance” and remains entirely describable by a collection of numbers, which appear to describe no more than themselves. It is therefore difficult to see how the world could actually be anything other than a collection of numbers. It is paradoxical that the Laplacian paradigm, often perceived as the epitome of “materialism”, actually dissolves the world into a substanceless abstraction.

A reversible determinism

The Laplacian model is deterministic, in a sense defined by the above quotation: the world is governed by a set of laws such that if I know its state at a given moment (the set of numbers that describes it), I can in principle deduce (calculate, compute) its state at any future moment. The word “determinism”, however, refers to something more, that includes the notion of a cause-and-effect relationship: that the state of the future world is entirely caused by its present state. This common interpretation is suggested by the origin of the word: the future is determined, that is caused, by the present, since a given present state can produce only one possible future state. It thus seems natural to equate physical, Laplacian determinism with a principle of total causality (“everything that happens is determined by what previously happened”); but paradoxically, as I shall show, the very notion of causality is an empty word in Laplacian determinism.

Significantly, Laplace's quotation gives the same role to the past and the future: “and the future, like the past, would be present to its eyes”. Indeed, all classical models of physics are reversible concerning time. This means, in graphic terms, that if I film any event, and then play the sequence backwards, the reversed sequence I see still satisfies the same laws of evolution. This property is verified in the “billiard ball” model: both the uniform rectilinear motion and the changes in motion during collisions are reversible.

This is a property shared by all current physical theories, including, with some qualifications, by quantum theories29.

Laplacian determinism implies that if I know the state of the world now, only one single state can follow at a given future time; but because of its symmetry between the past and the future, it also implies that the present state can stem from only one single possible state at a given past time. Does this mean that the present causes the past? The present “determines” the past as much as it does the future if by determination we mean that for a given present, there can be only one past, just as there can be only one future. And Laplacian determinism says no more than this. The notion of causality, which is always dissymmetrical – the past causes the future, but not the reverse – cannot, therefore, be founded on this basis alone.

This paradox illustrates the contrast between Laplacian reversibility and common sense: we do not feel that the past and the future are symmetrical at all. We view time as having a well-defined “arrow”, as being able to “move” only in one direction; and causes as being all on one side – which we call past – and effects on the other – which we call future. But it seems impossible to derive such an arrow from completely symmetrical evolutionary equations; the problem of the “arrow of time” has been one of the major difficulties of physics since the 19th century.

I will later return to the notion of causality because it is linked to that of laws – itself problematic in the Laplacian framework – and to that of free will, which I view as an unavoidable ingredient of the subjective.

The epiphenomenalist hypothesis

Epiphenomenalism is the idea that sentience (subjectivity, consciousness) is only an epiphenomenon of the physical world; that, in short, consciousness may “look but not touch”. This is less a thesis that anyone actually defends than the unpleasant conclusion to which many attempts to account for sentience within a Laplacian framework seem to lead.

I said above that because of the completeness of the Laplacian paradigm, our sensations, feelings and emotions are necessarily identical to certain “dispositions and movements of balls”, or, in the terms of a more realistic model, to the dispositions and movements of particles and the states of the fields inside our brains.

Intuitively, many people, including myself, find it difficult to believe that sentience can be “just” that. At the very least, it is not clear how particle movements and other “mechanical” processes can be a sensation; subjective sensations and phenomena seem to involve something more. I will return to more reasoned justifications for this feeling. Here I only want to note that if we try to make sentience into “something more” while remaining within the framework of the Laplacian model, we necessarily end up with an epiphenomenalist position.

Formally, the idea that sentience is something more than the movement of billiard balls directly contradicts the completeness hypothesis of the Laplacian model, which implies precisely that there is nothing more in the world than what this model contains. We can, however, imagine a “Laplacian-plus” model, consisting of what we may call the “physical” world, the world of the billiard balls, which would behave in a strictly Laplacian way, plus that “additional thing”, namely sentience, the seat of feelings. When fire burns my hand, for example, this would set in motion a succession of movements in the balls forming my hand, in turn influencing the balls in my brain, and lastly causing the balls forming my mouth to emit a scream; at the same time, the state of the balls in my brain would not itself constitute pain but would cause pain to passively appear in that “additional thing” where my sentience lies.

Such a conception, which appears capable of resolving our difficulty in conceiving sentience within the Laplacian framework, while maintaining this framework as a theory of the “physical world” (to which a mental world would nevertheless be added), necessarily implies epiphenomenalism. For it is assumed that sentience is affected by what happens in the Laplacian world; it is informed of pain, or, rather, of the dispositions of the billiard balls that correspond to pain. It does not seem impossible to give it such a passive position; but it is impossible to make it play an active role without violating, precisely, the determinism of the Laplacian world. The billiard balls evolve according to their state and that of the other billiard balls; it would be a departure from these laws to allow consciousness, our volition, to act on their evolution. And such a derogation cannot be accepted without bringing consciousness fully into the physical world, which would no longer be either Laplacian or “Laplacian-plus”30.

This is what leads us to consider the epiphenomenalist position, according to which consciousness is affected by the physical world while being in return unable to act upon it. Moreover, it appears to me that a certain number of positions that are current among philosophers who reflect on these issues imply epiphenomenalism. I have in mind in particular position B in Penrose's classification, which I will discuss in section 8, and which is the position of the philosopher John Searle. It is rare, however, that the defenders of these views explicitly embrace epiphenomenalism, because it is difficult to embrace consciously.

Epiphenomenalism implies that nothing in our behaviour is the result of our being conscious. This means that when we scream in pain, for example, we are not really screaming in pain; the pain, the desire for it to stop, and all other perceptions are felt by the spectatorial subjectivity but play no causal role in our screams, which result only from the non-sentient mechanics of “billiard balls”. Even the memories we believe we have of our own emotions are not memories of emotions, but the subjective effect of a present “purely physical” state “remembering” a certain past “purely physical” state, which, additionally, was (perhaps – how would we know?) producing a certain subjective state at the time.

If epiphenomenalism were true, we could not know it; or rather, we could not express it, or would only express it “by chance”. Epiphenomenalism is an attempt to explain consciousness, that is the fact that we feel things; but it precisely denies that our actions, and thus, in particular, our talk about epiphenomenalism, can in any way result from these feelings! Epiphenomenalism parks subjectivity on a one-way street.

More generally, if epiphenomenalism were true, we could know nothing of subjectivity; except perhaps of our own instantaneous subjectivity. We could not predict the consequences of our actions on our future subjectivity, since we cannot rely on any authentic experience of their past consequences. There would be no point in deliberating, doubly so: because we could not base our choices on anything, and because our choices could not affect anything.

If one accepts my thesis that we are deliberative beings, and cannot believe that deliberation is meaningless, one will accept that we cannot believe in the epiphenomenalist position.

It should be noted, however, that the definition I have given of epiphenomenalism depends on the notion of causality, which itself is problematic in the Laplacian framework. I do not want to develop this point here, but only to highlight the fact that epiphenomenalism, though tempting, is a false solution.

The Turing test

The name of the British mathematician Alan Turing is not well known to the general public, yet he is a major contributor to one of the central themes of science fiction and to the almost messianic expectations we have had concerning the “Year 2000”: the myth of the thinking, even desiring, indeed pathetic, robot such as HAL 9000 in 2001: A Space Odyssey. This theme presents the computer as an artificial equivalent of the human brain and suggests – more often than it asserts – that these beings, once they show themselves capable of behaving (more or less) like humans, are perhaps authentically sentient and thinking.

I call this a myth because at least for the moment it remains so. We do have machines today that we call “robots”, but they bear little resemblance to HAL or R2-D2. They are far from giving the impression that they really think, let alone that they have emotions.

It was in an article written in 1950 that Turing asked the question: “Can machines think?”31 He wondered about the definition of the terms “machine” and “thinking” and immediately replaced the initial question with another one, which he deemed “closely related”. Namely: “Is it possible for a machine to succeed in the ‘imitation game’?” This test, which Turing described at the time, has become known as the “Turing test”.

It involves having the machine “converse” remotely with a human, called the “interrogator”, who does not know whether he is dealing with a machine or a human being. The “conversation” takes place via teletype, the 1950s equivalent of our keyboards and computer displays. The machine can think, Turing says essentially, if it can deceive the interrogator in a conversation lasting several minutes and pass for a human.

Turing proposes to define thought as the ability to pass this test – at least this is what is suggested by how he introduces the test, as well as by several other considerations in the article. Other passages, however, as well as common sense, suggest that he does not propose the test as a definition; I will return to this issue. There is on the other hand no ambiguity in the way he defines a “machine”, as a computer, that is, as a device the behaviour of which is entirely determined by a program, or algorithm.

His view was that “in about fifty years' time it will be possible to programme computers (...) to make them play the imitation game so well that an average interrogator will not have more than 70 per cent chance of making the right identification after five minutes of questioning.”32 Year 2000 is behind us and this prediction has been proven wrong. Despite the technical power of computers, which far exceeds that predicted by Turing, and despite more than fifty years of effort by a large number of “artificial intelligence” research teams worldwide, no program on any computer is today capable of passing for a human being for even 30 seconds.

One may distinguish the three following claims in Turing's thesis:

(a) That one may validly define the fact that a system thinks by its passing such a test, that is, by its being able to exhibit the same behaviour as a human33.

(b) That the fact that a system thinks can be deduced from its behaviour.

(c) That a computer can indeed think, that is, can exhibit the same behaviour as a human being.

Statement (b) is an immediate consequence of (a): if thinking is defined by behaviour, it can certainly be deduced from behaviour. The converse is not true, however. Realism – the belief in the existence of a real world – implies that things exist by themselves, in one way or another, whether or not we have the means to ascertain this existence. This remains true even if we do, in fact, always have these means. Even if it were always possible to know whether it is daylight by looking out the window, the fact that it is daylight is not defined by the operation of looking out the window.

There is a view, called “operationalism”, which consists in asserting, on the contrary, that scientific notions must be defined by operations performed on the world. For example, the temperature of a body would be defined by the position of the mercury in a thermometer constructed in a certain way, brought into contact with the body in a certain way and for a certain time.

Operationalism is implicitly based on the separation of the world into humans and stones. For who is this “we” that is deemed to bring the world into existence, if not the set of all humans? Operationalism is a specific version of this separation, in which the stones do not actually exist by themselves; it is, therefore, incompatible with realism, and thus, in particular, with the Laplacian worldview, which presumes that the world exists. Yet the operationalist creed is part of the standard baggage of the modern scientific mind, cohabiting without too many clashes with the Laplacian paradigm. Here again, in fact, we have a sharing of fields of application; operationalism rears its head particularly in those fields of science that seem to escape the Laplacian paradigm, such as thermodynamics34, quantum mechanics and – precisely what interests us here – psychology.

It is the operationalist criterion that Schrödinger's “rationalist” uses to declare that the sentience or non-sentience of a non-human animal is without meaning: for we have, says he, no method to evidentiate it. Turing, on the other hand, states that in humans and computers, sentience does have meaning, but one that is no more than the success or failure at his test. Further on, he answers the objection that thought, emotion and other sensations are real things by asserting, in substance, that a denial of (a) implies that of (b) and must therefore be rejected35, because it would lead to solipsism.

Other passages, however, appear to imply that he does not actually take his test seriously as a definition of thought. For example, he wonders whether machines might “carry out something which ought to be described as thinking but which is very different from what a man does?”36, a form of thinking that would not be taken into account by his test. If one considers his test as a definition of thought, one cannot wonder if something else should be considered thought. Finally, his definition would lead to many humans being considered incapable of thought; a young child, a paralytic, a person who spoke no common language with the interrogator, etc., placed in the situation of the “machine” in the test, would not pass it any better than a stone; yet Turing does not seem to want to exclude such people. It seems, then, that he has in mind that his test is just that, a test, not a definition; a test implies the independent existence of the reality being tested and at the same time its accessibility (at least in principle) to experience.

I believe that Turing's hesitations reflect the impossibility of taking the operationalist view seriously, particularly in the field of psychology; for if we accept (a) and define sentience by an operation conducted by an observer, who, to observe, must himself perceive, hence be sentient, we obtain a circular definition. But if we reject (b), says Turing, we have no way of knowing whether a being is sentient; sentience can then only be ascertained by the person himself. This is why he claims that rejecting (b) would lead to solipsism.

My view is that we must indeed accept, essentially, (b), but reject (a); that is, we must accept that sentience exists per se and that at the same time, its existence cannot always be inaccessible to outside experience. It seems to me that we can arrive at this conclusion from the reasoning set out in section 4: if it were in principle impossible to determine “from the outside” that a being is or is not sentient, ethics would be impossible, just as physics would be impossible if it were in all cases impossible to determine “from the outside” the state of a physical system. We would find ourselves in the situation described by epiphenomenalism: an existing, real sentience devoid of any effect on the world.

However, I have not yet examined the link between ethics and sentience. I will return to this in section 8, to establish these conclusions more rigorously.

Note that accepting (b) in this sense does not mean that in every case it is actually possible to find out if a being is sentient or not. Neither was it possible for Galileo to map the far side of the moon; we may not be able to determine today whether flies are sentient or not. The dark side of the moon and the sentience or non-sentience of flies are nonetheless realities, which are not defined by the possibility that “we” might have of becoming aware of them. This double aspect of potential accessibility and inaccessibility is essential.

Why does Turing seem to believe that accepting (b) implies accepting (a)? It is certainly because he accepts (c), that is, basically, that it is possible to simulate by a computer – and thus by the execution of an algorithm – any behaviour of a sentient being. It is therefore impossible to distinguish from the outside such a computer from a sentient being. If we accept (b), then we must conclude that this computer is, indeed, sentient. But on the other hand, there is nothing in the computer's guts that seems to correspond to anything like sentience; we find only transistors and wires, and, at another level of analysis, algorithms determining behaviour. Above all, no theory exists that allows us to recognise sentience when we happen to encounter it; worse, within the implicitly accepted Laplacian framework, we cannot see what such a theory might look like – indeed, I think that within this framework such a theory is impossible.

If we are unable to find sentience in the computer but must accept that it is sentient (if it cannot be distinguished by its behaviour from a sentient being), we have no choice but to consider that it is sentient, and this on the basis of its behaviour alone; we must then, for want of a better option, define sentience operationally, by this behaviour.

If this is indeed Turing's underlying reasoning, it is made necessary by:

— his acceptance of (c);

— the impossibility of founding a realist theory of sentience within the Laplacian framework.

The reason to accept (c) is that it is a direct consequence of the computability of Laplacian determinism. It is this core point that underpins Penrose's position, which is that the true physics of the world cannot be computable, that is, we must reject (c). I agree with Penrose on this point; I think we should reject (c), which allows us to accept (b) as a test of sentience, viewed as a real object of the world rather than as something defined by the test as asserted in (a).

We have seen that (c) has not been shown true within the time frame predicted by Turing, but this does not in itself imply the falsity of this proposition. It is for other reasons, which I will develop in section 7, that I believe that it is not possible to simulate the behaviour of a sentient being by an algorithm and that therefore the world cannot be computable. Before doing so, it will serve to better describe this notion of computability, and to distinguish it, following Penrose37, from the more general notion of determinism.

Computability

Determinism implies that if the state of the world is specified at a given moment, its state at a future moment is determined. Computable determinism further implies that this future state can be computed. One may have the impression that this adds nothing and that determinism is necessarily computable, but this is not the case.

In the Laplacian model, the world can be described at each moment by a collection of numbers. The laws of evolution allow us to calculate, given these numbers at time t, their new value at an immediately subsequent time t + dt. This calculation can be broken down into elementary arithmetic operations (addition, multiplication...), which can be done by applying simple “recipes”, that is, automatically; in short, by an algorithm. In fact, for several reasons it is rarely possible to perform this calculation with perfect precision; for example, it would have to be done with an infinite number of “decimal places”. However, it is always possible to do it with as much precision as one wants, at least in principle38.

The notion of an algorithm was formalised rigorously by our same Alan Turing, as being any operation of which a certain type of machine, now called a “Turing machine”, is capable. I will note the main points39. The Turing machine has a program, which represents the particular algorithm it is to execute; this is a finite (but as large as you like) list of instructions. It is provided with a set of starting data; in this case, the description (as precise as we like) of the world at a certain time t₁. By running its program, it transforms this data step by step. After a certain time (as long as necessary) it reaches a “stop instruction”. The data it then leaves behind is the result of its execution and will represent, in the case we are interested in, the state of the world at another time t₂ (with as much precision as desired).

Note that the algorithm is given, independently of the data. With this one algorithm, we can obtain, from any possible state of the world at t₁, its state at t₂.

Two features of this procedure are important here:

— Necessity. If the world at time t₁ is in a certain instantaneous state I₁, then at time t₂ it is necessarily in another, determined, state I₂.

— Computability. If I know I₁, I can calculate the state I₂ using an algorithm established in advance (an algorithm independent from I₁).

It happens to be the case that these two notions are not identical; more precisely, necessity does not always entail computability. In the case of Laplacian physics, both are true. There are, however, classes of mathematical problems in which every particular problem in the class has a precise, necessary answer; but where no algorithm exists, or can exist, that allows this answer to be obtained “mechanically” for all problems in the class.

Penrose gives as an example of such a class of problems the tiling of the plane with geometrical “tiles”, such as the three in Figure 340. The question here will be: is it possible, with these three tiles alone, cloned indefinitely, rotated and/or flipped over at will, to completely tile the infinite plane, without overlaps or holes? It turns out that for the set of tiles in Figure 3, the answer is yes: it is possible to do so. On the right of Figure 3, there is a possible start of such a tiling. However, there happens to be no periodic tiling in this case, and the proof of the positive answer is not trivial, though it exists.

For other such sets of tiles, the answer will be negative. What is important to note is that for each set of tiles (hence: for each problem in the class of problems) the answer is perfectly well defined: the tiling is possible or it is not. Here we find the notion of necessity; we can say that the specification of a set of tiles makes necessary, or determines, the “yes” answer, or the “no” answer.

It has been shown, however, that this answer is not computable; that is, there is no algorithm, no recipe that can be applied mechanically, that can tell, for any given set of tiles, whether it can or cannot tile the plane. Certainly, for any given set of tiles, there exists an algorithm for that set that gives the right answer; indeed, since that answer is either yes or no one of the two elementary algorithms “answer yes” and “answer no” perforce does the job! What does not exist is a single algorithm, common to all sets of tiles (to all problems in the problem class), capable of giving, for each of these sets, the right answer.

Given a set of tiles, how can we determine, therefore, whether it tiles the plane? The only possible answer is: “Look for a proof!” (of a positive or negative answer). In other words: “Think!” But this “recipe” is not guaranteed to work. We cannot know in advance, in the general case, either that we will succeed or that we will fail. No mechanical recipe can tell. And if we find a proof, for the next set of tiles we will have to start over; each proof will be an innovation.

This tiling problem shows the distinction between necessity (determinism) and computability. Penrose, on this basis, imagines a “universe” (not a plausible one of course) subject to a deterministic but non-computable law of evolution. The state of the universe is simply represented at each moment, not by a collection of numbers as in the Laplacian model as described above, but by a set of tiles. The evolution law is such that the state of the universe at time t + 1 depends on whether the set of tiles corresponding to time t tiles the plane or not. Such a law is deterministic, in the sense that at each instant the set of tiles that describes the state of the universe does or does not tile the plane; thus the next state is determined. It is not, however, computable, since no algorithm is such that given any state at time t it can predict the state at time t + 1. A computer, for example, would be unable to predict the evolution of such a world, despite it being determined.

The Laplacian model of the world is deterministic and computable. Penrose's thesis is that the evolution of the physical world cannot be computable. On the other hand, he seems to accept that it must be deterministic, like the fictitious tiling world that I have just described; it will of course be much more complex, incorporating all the current physical knowledge as an approximation. Penrose looks for such non-computability in a relationship between gravity and the “wave packet reduction” problem in quantum mechanics; and notes the existence in some nerve cells of very particular structures suggesting the possibility of such phenomena inside them41.

The constructive part of Penrose's ideas is very interesting but is far from forming a complete theory. Nor does it in any way provide a characterisation of sentience as such, that is of the fact that we feel things rather than their merely “happening” in a non-sentient way. In section 6, I will seek to detail some questions about the very structure of the physical world that again appear to result from certain facts that we cannot nonbelieve. In this context, it may not seem evident that the world is deterministic at all, even in a non-computable way.

In any event, the very possibility of non-computability, which is a fact of mathematics, is quite suggestive, at least by the parallel that can be made with the deliberative situation I mentioned in section 4. We believe in the existence of a right answer to the question “What to do?”; this answer is determined, “exists”, perhaps in the same sense as exists, for a given set of tiles, the right answer to the question “Do they tile the plane?”. How do we arrive at this correct answer? In the case of tiles, there is no recipe; we have to think. I suggest that the same is true for the deliberative situation. To answer the question “What to do?”, we have to think. In either case, we know that the right answer exists, but we usually have no recipe for finding it. Nothing assures us that we will succeed, but nothing either makes it certain that we will fail.

This distance between knowledge and its object is perhaps essential for the existence of both. What is striking about models of computable determinism is that the result can be obtained by an algorithm, that is by a process in which this relationship between knowledge and its object, a relationship known as “intentionality”, is unnecessary and, in fact, is absent. The data manipulated by the algorithm needs no meaning for the computation to proceed and to lead with certainty to the correct result. The algorithm represents a kind of “thought without substance”. Non-human animals are often described as governed by mere “drives”. The drives directly determine behaviour; there is no need for the animal to understand anything, to decide anything, and therefore to desire anything: the drive could be directly connected to the muscles! Of course, there may be a conflict between multiple drives; for instance, the view of a watering hole together with the smell of a predator. Flee or go drink? According to this conception, the stronger impulse wins. Again, there is no need for thought; a three-neuron drive-weighing machine would be enough. There is no need to understand that there is a predator, to anticipate danger, to feel fear and a desire for water, to consider the existence of alternative water sources; there is no need for an intentional relationship, a feeling, a substance...

I am aware of the vagueness of these words; what is this “substance” I am talking about? Nonetheless, this “lack of substance” may be central to the difficulties our science has in accounting for sentience. Our feelings are things that exist as such; but science seems to want to admit only empty things, which exist only in relation to other things that are themselves empty.

The “substance” I am talking about is perhaps simply existence. But how do we define the fact of something existing? What seems certain is that if we take the Laplacian model seriously, the word “existence” appears very hollow. To see this, some formalisation of the model's conceptual framework will be useful.

The conceptual framework of the Laplacian model: real world, possible worlds, imaginable worlds

The Laplacian model implies that the world as a whole can be described by a mathematical object. In the billiard ball example, this description will be the enumeration of the three position coordinates and corresponding three velocity coordinates of each of the balls at a given moment; hence, if n balls exist in the universe, it will be a sequence of 6n real numbers. The world is therefore entirely described by this sequence, that is, by an element of the set noted ℝ⁶ⁿ of all sequences of 6n real numbers. Everything that can be said about the world at this instant is encapsulated in this object, and the knowledge of the world at this instant allows knowledge of the world at all past and future instants, in other words of the whole world over its entire history.

I will therefore distinguish the instantaneous world – the whole universe at a given moment – from the historical world, which is the whole universe in all of its past and future. This notion of a historical world may appear fictitious; we may want to ask, “When does it exist?” Yet we might also ask about the instantaneous world, “Where does it exist?”, without the lack of a possible answer making in this case the notion of an instantaneous world fictitious. Must an object exist at a time, but not necessarily at a place? Here is an illuminating remark by Penrose42:

Consciousness is, after all, the one phenomenon that we know of, according to which time needs to “flow” at all! The way in which time is treated in modern physics is not essentially different from the way in which space is treated and the “time” of physical descriptions does not really “flow” at all; we just have a static-looking fixed “space-time” in which the events of our universe are layed out! Yet, according to our perceptions, time does flow (...).

What Penrose says here specifically concerning modern physics applies to the Laplacian model in general43. In this view, if the world is a reality, then the historical world is the totality of reality, even if this notion goes counter to our intuitions. If, as I believe, our intuitions in this matter are actually correct, then it is the Laplacian model itself that we will have to reject; meanwhile, since we are examining the Laplacian model here, we accept the historical world as real.

Since we can describe the instantaneous world by a mathematical object I belonging to a certain set I – in the case of billiard balls, I is the set ℝ⁶ⁿ – we can also describe the historical world by a mathematical object M, belonging to the set M of mappings that make any date t correspond to an instantaneous world I = M(t).

We thus have two sets: the set I of all imaginable instantaneous worlds, to which at every moment the real instantaneous belongs; and the set M of imaginable historical worlds, to which the single real historical world M_R belongs – the subscript “R” marking that it is the real historical world.

A graphical representation of this can be given if we imagine the set I of imaginable instantaneous worlds as plottable on a straight line; this is an extreme simplification, since in reality, even in the simple case of a world of billiard balls, not one but a large number (6n) of dimensions would be needed to represent this set; but it allows us to draw a two-dimensional graph, with the instantaneous worlds on the ordinate and time on the abscissa (Fig. 4).

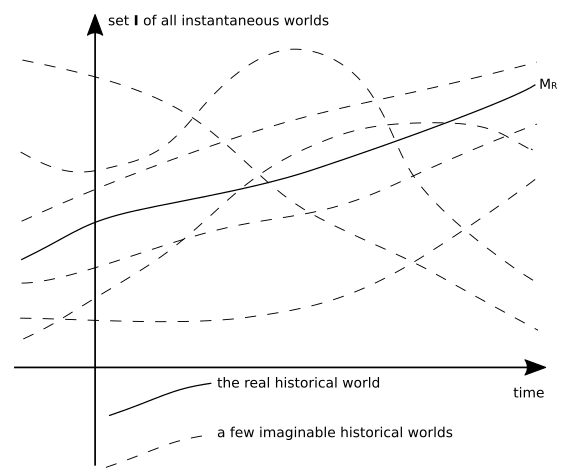
The real historical world M_R is then represented by a curve, describing the succession of instantaneous worlds that arise over time. In Figure 4, this is the thick solid curve. The dotted line represents some of the innumerable conceivable historical worlds; any arbitrary succession of instantaneous worlds is a conceivable historical world but only one of these successions corresponds to the real historical world.

What is the status of the laws of physics within this framework? They allow us to deduce the real state of the world at any moment in the past or future, provided that we know the real state at the present moment. If we know that at time t₁ the world is actually in state I₁ we can deduce the instantaneous state I₂ of the world at any other time t₂. Knowing I₁, we can therefore deduce the real historical world in its totality; we are in the position of the “intelligence” of which Laplace speaks, to whose eyes “the future, like the past, would be present”.

However, these laws tell us more than that. The law of gravity, for example, tells us not only how the planets will behave in the real world orbiting the real sun, but also how they would behave if they were placed differently than they actually are, or if the sun were twice as massive, and so on. The laws of physics thus allow us not only to deduce the real state I₂ of the world at time t₂ from its real state I₁ at time t₁, but also to deduce the instantaneous state I'₂ that the world would have at time t₂if it was in any other instantaneous state I'₁ at time t₁ (Fig. 5). In short, they allow us to trace not only the trajectory corresponding to the real historical world, but also a whole family of trajectories corresponding to historical worlds that are not real, but that conform to these laws in their evolution and that I will therefore call possible historical worlds. I have represented two of these possible (but not real) historical worlds in Figure 5, by densely dotted curves. These curves do not cross each other, which reflects the determinism of the laws (only one possible historical world passes through a given point).

The laws of physics thus appear as rules specifying a set of “possible” historical worlds among a larger set, that of the imaginable historical worlds. I can imagine that the world evolves in any way; that after jumping out of the window, for example, I fly away like Superman. Any succession of states of the world is imaginable. It is the laws of physics that say that if I jump out of the window, I will fall rather than fly; thus the world where I jump and fly is imaginable, but not possible. The world in which I jump and fall is possible, but not real (because in fact, I will not jump).

A limited determinism

The idea that things could happen without reason seemed shocking when quantum mechanics was formulated in the 1920s; this sense of outrage persists and explains part of the nostalgia for the old framework that persists today. All of a sudden, it appeared that there were unanswerable questions, events that happened “by pure chance”, “out of the blue”. Hence Einstein's protest that “God does not play dice”. Within the Laplacian framework, everything seemed to have a cause. The state of the world today was caused by the state of the world yesterday, and so on, ad infinitum. Each “why?” had its “because”.

Yet in the Laplacian model itself, there is a “why?” – and not the least – that does not have its “because”. This is worth noting if only to instil some doubt into our attachment to absolute determinism, and open our minds to other possibilities.

In the Laplacian framework, our “why” questions are always answered as long as they relate only to instantaneous states of the world or of subparts thereof. The laws of evolution infallibly determine the instantaneous states of the real world in relation to each other. But if we consider this succession of instantaneous worlds as a whole and thus fix our attention on the real historical world M_R, there is nothing in Laplacian determinism that tells us why the real world must be this one, rather than any other possible historical world. When the dice are thrown, it explains the outcome by the initial position and velocity of each die, but it does not explain why we are in this world, with these initial positions and velocities and this outcome, rather than in another, with other initial positions and velocities and another outcome.

To those who claim that God exists because the world must have a cause, rationalist atheists often reply that the cause of the world today is the world of yesterday and so on. The explanation by God is a non-explanation; but we see that the same is true of the explanation of today by yesterday. Laplacian determinism does not provide us with an answer to these questions any more than belief in God does.

6. Causality, Freedom and Physical Laws

Based on this same principle of the impossibility of certain nonbeliefs, I come to two consequences that have a direct bearing on physics, because they directly contradict the Laplacian worldview.

The first of these consequences – the reality of the causal relation – is usually taken for granted, and viewed as evidently compatible with the Laplacian worldview; it would even be almost tantamount to the notion of determinism that underlies this view. The second – the reality of our freedom, or free will44 – is taken for granted in everyday life, and in the practice of courts45, but is paradoxically seen as incompatible with the Laplacian view, which would however imply that we have the illusion of it being real.

I believe that causality is real, but that, contrary to the common view, its reality is incompatible with Laplacian determinism. I also believe that free will is real and that it too is incompatible with the Laplacian view.

Additionally, these two notions are related to physical laws. These are in the same situation as causality: they too are, contrarily to what is commonly believed, incompatible with Laplacian determinism. Yet they cannot be abandoned.

We must build a physics that accepts the reality of causal relationships, free will and physical laws. Such physics cannot, therefore, be consistent with Laplacian determinism.

Causality and determinism

Causality implies a certain relationship, called “of cause and effect”, between two events. This is not just a juxtaposition. Élodie threw a stone out the window (event A) while pronouncing “Pumpkin!” (event B). The stone fell on the street (event C). We will say that A was the cause of C, but we will not say that B was the cause of C.

Why not? The simple answer – and a good one, I think – is that if Élodie had not thrown the stone, it would not have fallen on the street. We will not say the same of B: that if Élodie had not uttered “Pumpkin!”, the stone would not have fallen on the street46.

But what can these statements mean? They are counterfactual assertions, that is, they speak of events contrary to the facts. In the world that exists – the only world, that we noted M_R in section 5 – Élodie threw the stone, and said “Pumpkin!”. To talk about what would have happened if Élodie had not done these things is to talk about a world that does not exist. What can we say about a world that does not exist?

One can, of course, imagine it. The counterfactual statement C1: “If Élodie had not thrown the stone, it would not have fallen on the street” refers to a world we can imagine where Élodie does not throw the stone and it does not fall on the street. We find it logical to imagine such a world; indeed, we give it, as it were, a status of partial reality, by considering as true this “If... then...” counterfactual statement.

Can we do the same for the other counterfactual assertion, the one that we reject, namely C2: “If Élodie had not pronounced “Pumpkin!”, the stone would not have fallen on the street”? Of course, we must assume that “all other things are equal”, in other words, that Élodie throws the stone (as she does in the real world) but refrains from uttering “Pumpkin!”.

We can indeed imagine such a world satisfying C2, that is in which the stone, rather than falling on the street, floats in the air, for example, and returns by itself to land on the table. This world is perfectly imaginable (you have just imagined it); is this enough to conclude that if Élodie had not said “Pumpkin!”, the stone would not have fallen on the street? Of course not.

It is therefore not enough that we can imagine an alternative world in which a statement is true to allow us to view it as a true counterfactual assertion. This alternative world must also appear possible, in the sense I gave this term in my above description of the Laplacian model. The imaginary world satisfying C1 is consistent with the laws of physics, and in particular, with the law of gravity. In a world satisfying C2, instead, the stone floats in the air, which contradicts the laws of physics; C2 is only “imaginable”, not “possible”.

Does this solve the problem? I do not think so. For it implies that one must give the notion of a physical law a higher status of reality than that of the real world itself. If the M_R world is all that exists, physical laws cannot have such a status.

What are these physical laws? In the Laplacian perspective, only the M_R world exists. However, it is not just any world: it obeys certain physical laws. These laws appear as a collection of “regularities”. We have seen in the past that every stone, once dropped, falls. Without this regularity, to describe M_R, we would have to list how the stone behaves every time we drop it. Thanks to this regularity, one sentence is enough.

Generally speaking, the laws appear in the Laplacian framework as the expression of the somewhat “miraculous” fact that this historical real world – this succession of an infinite number of instantaneous worlds – can be “summarised” by the knowledge of any one of these instantaneous worlds, with the addition of a few relatively simple laws of evolution.

This conception of laws – the only one possible, it seems to me, within the Laplacian framework – runs up against three difficulties, the first two of which have long been recognised:

— How is it that such a summary is possible?

— How can we, from the observation of these past regularities, deduce that they will still be verified in the future (the induction problem)?

— If the laws are no more than that – the observation of regularities within M_R – they tell us nothing about other worlds.

I believe that these three difficulties are linked, but I leave aside the first two; the third is enough for my purpose. If the law notes a regularity and predicts the repetition of the same regularity in the future, it can tell us that when the rock will have been dropped by Élodie, in the real world where she utters “Pumpkin!” at the same time, it will fall. It still says nothing about another world, which doesn't exist!

We might want to consider that these laws can tell us about these other worlds, as it were, by extension. Similarly, we can say that “since half of any number divisible by four is even, if ten were divisible by four, five would be even”. However, it turns out that the same reality – that of the unique M_R world – can be described by different sets of laws. We can also state that “any number divisible by four minus five is odd”; hence if ten were divisible by four, then ten minus five, that is, five, would be odd! The same applies to physical laws.

For example, we can state the following law:

Every time a stone is dropped, it falls, unless “556841278025 pumpkins!” is pronounced at the same time, in which case the stone floats.

It happens to be the case that in M_R these exact words are never uttered when a stone is dropped; or if they are (you can, now that I have stated this law, make it false!), an infinite number of other such sentences are not. Let us suppose, then, for the sake of argument, that this is the case with this one. This law is then true. Moreover, it satisfies all the desired criteria of regularity. It has as much validity as a law describing M_R as has the usual law, which says that the stone will fall in all cases.

Yet the usual law, and this modified law, disagree about what would have happened if Élodie had uttered “556841278025 pumpkins!” while dropping the stone: the usual law predicts that the stone will fall, and the modified law specifies that it will float. So we cannot say, based on the laws, what would have happened in this case. Therefore, we cannot determine whether Élodie's failure to say this sentence is, or is not, the cause of the stone falling.

It may be objected that this modified law is more complicated than the other; that the simpler law “prevails” (a criterion referred to as “Ockham's razor”). This seems sensible; but in what sense does the simpler law “prevail”? This criterion is undoubtedly good as a heuristic principle; it does not change the fact that neither the usual law nor the modified law can be “tested” in a world that does not exist, the world in which the sentence would be uttered; and only that world might decide between them.

So where does this leave us? We can say that it does not matter what would have happened if the world had been different. Laws govern what happens in the real world; what would happen in another world is a question of convention. The same goes for the cause of an event; if A, B and C happened, it doesn't matter whether A or B caused C; what matters is that they happened!

Can we accept such a conclusion? I think not. Causality is a fundamental concept in our daily lives, as is the notion of law. For the courts, for example, it is not irrelevant whether it was the action of one person or the word spoken by another that caused, say, a stone to fall on the policeman's head! This attribution of responsibility by the courts simply reflects the fact that each one of us – of us, I would say, sentient, deliberative beings – chooses our actions depending on their consequences. To do so, we must believe in future causality at the moment of deliberation.

We have already noted another difficulty with the notion of causality in the Laplacian model, which is its asymmetry concerning time. The cause necessarily precedes the effect; this seems to be an absolute, even definitional, rule of the notion of cause. However, we have seen that in the Laplacian model, time does not have an “arrow”: the same laws remain true if the direction of time is reversed. In particular, if an “intelligence”, as Laplace put it, knew the present entirely, then “the future, like the past, would be present to its eyes”. This seems to suggest that there is no objective existence to the notions of before and after. Laplacian determinism is such that if the world is, at time t₁, in an instantaneous state I₁, at time t₂ it must be in some determinate state I₂; in this sense, one can say that the state at time t₁ determines that at time t₂. The reverse is also true, however: the state at time t₂ determines the state at time t₁; indeed, I have not specified the temporal order of t₁ and t₂.

It is not in such a weak sense that we generally understand the concept of determinism. By this word, we mean that the future is determined – completely determined – by the past. That it is caused by the past. The verb “to determine” has, in everyday language, almost the same meaning as “to cause”; and determinism is often presented as a theory of absolute causality. We have seen that we cannot give such a meaning to Laplacian determinism; in the Laplacian worldview, the world simply is; there are no causes and no effects. Ironically, it is precisely in this framework, that is perceived as deterministic par excellence, that the notion of causality loses its status as a reality.

This makes sense, however, if one perceives that the notion of determinism, or causality, is double-sided: there is a “necessity” ingredient and a “freedom” ingredient. “Determining that...” is also “choosing that...”. Élodie determines that the stone will fall on the street by her choice to throw it out the window; she could have refrained from doing so. The aspect of necessity in the notion of determination is that which follows this act, and which inexorably leads the stone to fall. Without this necessity, there would be no freedom of choice. When we say that the present determines the future and are reluctant to consider that it could also be the other way around, it is because we believe we can act, at least to some extent, on the present, and thereby modify the future. We cannot directly act on the future, and thereby modify the present. Élodie cannot directly cause the stone to fall in ten seconds on the pavement, and thereby cause her hand to throw it now.

The reason why Laplacian determinism dissolves causality, and thus represents determinism only in a weakened sense, is precisely because of how absolute its triumph is. If all is determined, nothing can determine.

In particular, in Laplacian determinism, we ourselves are determined. Determinism is often felt to be in contradiction with the traditional notion of free will; if “all is written”, nothing can be chosen. To this, the rationalist tradition often replies (“compatibilism”): everything may well be written (i.e. determined), but since we do not know what is written, we cannot escape the necessity of choosing, even if the result of this choice could be known in advance by a Laplacian “intelligence”. I long believed in the validity of such an answer; I do no more. On the contrary, I think that there is indeed an incompatibility between the notion of freedom and Laplacian determinism. Again, this stems from taking the internal point of view seriously, and the principle of founding by the impossibility of nonbelief.

Dessert or tofu?

Let us take another look at the deliberative situation. Suppose that we are in a restaurant and have the choice of ending our meal either with a dessert or with tofu. Let us assume that Laplacian determinism is true. The choice we will make is then determined by the initial conditions, by the arrangement of atoms in our brains. Suppose this will lead us to choose dessert. Then we can't take tofu. Better still, “can” and “can't” are meaningless; in the real world, the only world that exists, we will take dessert.

Yet, as we deliberate, we are fully convinced that we can choose tofu and that we can choose dessert. This is the very basis of our deliberation. It is not just that we do not know what we will have. Suppose we are told that whatever we decide to ask for, the cook will do as he pleases; he will give us the dessert or the tofu, depending on what he has most available. Again we don't know what we will get, but this time deliberation seems pointless. So it is not the uncertainty alone that underlies the deliberation, but the feeling of being able to make one of the choices or the other.

Now suppose instead that we are told that the cook has already determined what he will prepare for us, but this time it is a more helpful cook. When we entered the restaurant, he scanned our entire body, and he also knows, with all the necessary precision, the environment that is the restaurant. By the laws of Laplacian determinism, and using his state-of-the-art personal computer, he calculated that we would choose dessert. This is all possible, in principle, within the framework of Laplacian determinism.

Now suppose we know all this; we are even told that the choice we are going to make is written inside a small folded paper on the table. The future is literally written. What would then be the point of deliberating? We don't know what is on the paper, but we know that we are not going to change it anyway! We can rest our minds, and wait to be served!

This, one may object, contradicts our premises: for the cook has foreseen that we will deliberate and choose dessert. His Laplacian calculations should have told him instead that his client, informed of the presence and significance of the folded paper on the table, would refrain from deliberating. The cook would then not have known which choice to write on the piece of paper!

The problem is that he can come to the same conclusion about each of us, as long as we believe in Laplacian determinism; and this is true, whether or not the future is physically written on a piece of paper! If we believe in Laplacian determinism, we have no motivation to deliberate. Yet we do deliberate. I think this means that we do not believe in Laplacian determinism.

I also believe that this means that we cannot believe in Laplacian determinism. For we can but deliberate; even the choice to “rest our minds” involves initial deliberation.

The attempt I have described to reconcile Laplacian determinism with the logic of the deliberating individual only works as long as we don't actually take the latter's viewpoint seriously. The description of the individual in terms of billiard balls has its internal consistency. But there is nothing in this description that corresponds to being able to make a choice. Billiard balls can nothing; they only do. At most we might find, assuming that sentience, beliefs, etc. are “emergent properties” of a Laplacian system, something within the nervous tissue that is the belief in our possibility of choice; but finding the belief in x is not finding x. The Laplacian view may agree that we believe; it does not agree with what we believe. It cannot be ours; we cannot believe it to be true.

Newcomb's paradox

This well-known paradox was formulated by the physicist William Newcomb in 196047. I will give a slightly modified version, which, assuming Laplacian determinism, leads to a contradiction.

We will once again assume that there is a Laplacian “intelligence” which, together with its calculator, is capable of predicting our actions. This time instead of a cook it will be a Zlork, who has come from the Andromeda Galaxy to test an Earthling, called Noumène.

It is a test in which Noumène can only win, but how much she will win will depend on the choice she makes.

Noumène is taken to a room where there are two closed boxes. The rules of the game are then explained to her. Each box contains a certain sum of money. Noumène can choose to take both boxes or just one; she will open them only once she has made her choice. The sum of money in each box was determined the night before by the Zlork as follows:

— if the Zlork anticipated that Noumène would take both boxes, he placed ten złoty in each;

— if the Zlork anticipated that Noumène would take only one box, he placed one thousand złoty in each.

The Zlork made this prediction the day before based on the information acquired by scanning Noumène, as well as the entire environment with which she would come into contact in the meantime; including the environment to which she would be exposed in the room where the test takes place. He could not, of course, take into account in these calculations the amount of money that the boxes would contain, since this depends precisely on the outcome of his calculations; but since this amount is not communicated to Noumène before she makes her choice, it cannot affect her behaviour. The Zlork, therefore, has all the information that could determine Noumène's behaviour, and can therefore, if Laplacian determinism is true and his calculator sufficiently powerful, predict, with certainty, that behaviour.

If Laplacian determinism is true, then all this is, at least in principle, possible.

Noumène, being a typical Earthling, wants to win as many złoty as possible. She knows the rules of the game. What should be her choice?

Answer (1): Her interest is to take both boxes. If she takes both boxes, she is bound to get twice as much as if she takes only one.

Answer (2): Her interest is to take only one box. The box will contain one thousand złoty since the Zlork will have foreseen her behaviour and will have put this amount in it; on the other hand, if she takes both boxes, each will contain only ten złoty, for the same reason; she will therefore win only twenty złoty, which would pain her.

I believe that both of these arguments are unassailable. The first is the one that Noumène would already make in the ordinary conditions in which no one has foreseen her actions. It is based on a certain limited degree of causality, in which the choice of taking one or two boxes does not change their content. The second is dependent on Laplacian determinism; more precisely, it is dependent on Noumène's belief in this determinism. It is based on another causality, whereby Noumène's choice determines the contents of the boxes, by determining backwards in time the sum that the Zlork has placed in them!

In the framework of Laplacian determinism, it is impossible to decide which of these two causalities is the “real” one; for only one world exists, in which everything happens but nothing causes.

The contradiction that Noumène arrives at concerns two prescriptive statements: (1) “Take both boxes!” and (2) “Take one box!” The contradiction vanishes, of course, if we refuse to consider that the prescriptive statements have any real meaning; if they are but illusions, the contradiction is but illusory. Again, it is because of the impossibility of our nonbelief that prescriptive assertions have real meaning that we must reject the assumptions that allow the existence of such contradictions. More specifically, I think it is necessary to reject the assumption that it is possible, even in principle, for a Zlork to predict, using a computer or by any other means, the choice we are about to make. We must therefore, at the very least, reject Laplacian, computable determinism.

Why Élodie does not jump out the window

A third case will show more clearly the need to attribute some form of reality to counterfactual worlds. Let's assume that Élodie is on the top floor of a skyscraper. The window is open. Élodie has no suicidal tendencies. Why doesn't she jump out the window?

The answer seems obvious: she doesn't jump out the window because if she did, she would fall and die.

However, she has no intention of jumping and knows it. So what reality can she give the sentence “If I jumped out the window, I would fall and die”?

Here we are back to the contradiction previously mentioned concerning the cause of the stone's fall; but this time, we are concerned with future events rather than past ones. Élodie is faced with the choice of jumping or not; if she doesn't jump, it's because she believes the sentence “if I jumped, I would fall” to be true. If she believes it to be true, it is because it describes something real. If, however, the world in which Élodie jumps is in no way real, this sentence can have no meaning, and thus cannot be true.

Deliberation is a situation where we face several possibilities. We have to believe in the reality of these possibilities, and in the consequences each of them will lead to, for our deliberation to make sense. This implies attributing a reality of some kind to all these future situations. This remains true even in cases when our mind is already made up, such as when Élodie is in the room with the open window, as long as we retain the possibility of choosing otherwise. Élodie is free to jump, even if she has no intention of doing so. Because of this freedom, the situation in which Élodie will jump retains a certain reality, and it is this reality that gives meaning to the assertion she necessarily believes: “If I jumped, I would fall.”

The deliberative situation that is ours thus implies that we believe in our freedom. This freedom is a reality even when our choice appears obvious. It is this freedom that gives a sense to the deliberative situation, but also to causality and physical laws.

Let us return to the situation of Élodie with her stone, but at a moment when she hasn't yet chosen what she will do. She can choose to throw the stone while saying “Pumpkin!”; to throw it without saying anything; to say “Pumpkin!” without throwing the stone; and finally, to do neither. If we assume that these four possible future worlds are in some way real, it is unambiguously that we can say that the act of throwing the stone, but not of uttering “Pumpkin!”, causes it to fall. The reason is that in both of the worlds in which Élodie throws the stone, it falls, whether or not she pronounces “Pumpkin!”; in the other two, it does not fall.

If we cease to limit physical laws to a description of one single world M_R but require that they describe a plurality of possible worlds, their arbitrary character disappears. Since we can say “556841278025 pumpkins!”, as well as all similar sentences, even if we have no intention of actually doing so, the worlds in which we utter these sentences have each a measure of reality; in each of these worlds, the stone falls (despite our sentence), and therefore none of the modified laws I have suggested – where uttering such a sentence causes the stone to float – is true.

The extravagance

I am aware that these conclusions are both “extravagant” and ill-defined. What can this “partial reality” mean? This “plurality of worlds”?

I have chosen not to delve here into the question of quantum mechanics. I will simply state the following points, which any specialist in the field will recognize as true:

The postulates of quantum mechanics possess, in the eyes of common sense as well as in those of our Laplacian habits of thought, a quite extravagant character.

Quantum mechanics implies, or at least strongly suggests, the possible existence of a “plurality of worlds”; be it the evanescent quantum superposition limited to the “microscopic” world, the enduring but fragile plurality of worlds of the “Schrödinger cat” type, or the limitless multiplicity of many-worlds theories (Hugh Everett).

Counterfactuality has a different status in quantum mechanics from its (non-)status in the Laplacian perspective; in some experimental setups, counterfactual assertions even appear testable.

The standard (“Copenhagen”) interpretation of quantum mechanics empties the notion of reality of its meaning; if we want to reconstruct this notion, it seems conceivable that it would be quite different from what we have now.

The standard “Copenhagen” interpretation of quantum mechanics gives a key role in lifting the quantum superposition to the notion of an observer. This notion is actually not defined within this interpretation (or is implicitly defined as a human being), but its most immediate interpretation in realistic terms is that of a subjectivity. The standard interpretation avoids this conclusion only by dispensing with the very notion of reality.

I certainly do not, however, claim that quantum mechanics, a non-Laplacian theory (in its standard interpretation) gives us a solution to the problem of the reality of ethics, free will and other subjective ingredients. On the contrary, it is by starting from the subjective that we have reached our conclusion about the impossibility of nonbelief in the existence of a reality, of a “something”; an existence that the standard interpretation of quantum mechanics precisely denies. Moreover, quantum mechanics in this interpretation does not give substance to an enduring plurality of worlds. Finally, the many-worlds interpretation, the one that would seem to better suit some of our conclusions, is a return to a Laplacian framework; we have seen that this precisely doesn't work48.

We can view the points listed above more as clues in a detective story; as elements suggesting that we are on the right track, without yet knowing how to assemble them into a full picture.

Penrose does not believe in the many-worlds interpretation at all. Instead, he has discerned within the nervous tissue certain very specific structures – called microtubules – which, according to him, are capable of maintaining quantum coherence (between “multiple worlds”) for long enough for certain phenomena to come into play. These phenomena are linked to quantum gravity, which he assumes to be deterministic but not computable49; they would produce the “wave function collapse” and thus, as it were, a non-computable choice of the real future world among the various possible ones. This is reminiscent of our deliberative situation, which obliges us both to make sense of a multiplicity of future worlds and to choose among them.

Again, these considerations do not form even a sketch of a complete and satisfactory theory. However, they do suggest at least this: it may be that certain features of the subjective are part of the fundamental laws of physics, with the nervous tissue representing a privileged locus for the use of these laws for the efficient resolution of the problems that an organism must face to survive, and that subjectivity itself, with its qualia, pleasures and pains, results from this use.

7. The Reality of Sentience

(...) as I observed that this truth, I think, therefore I am, was so certain and of such evidence that no ground of doubt, however extravagant, could be alleged by the sceptics capable of shaking it, I concluded that I might, without scruple, accept it as the first principle of the philosophy of which I was in search.50

If in this Cartesian approach, we replace the act of thinking with that of simply perceiving, we can argue that our own sentience is a self-evident fact, and that consequently sentience itself exists as a fact of the world. This self-certifying sentience is, however, somewhat autistic; Descartes is subsequently obliged to appeal to the notion of God to try to prove the existence of the world itself.

We have seen (section 4) that all action, all deliberation, is fundamentally altruistic, in the sense that it is not concerned with the individual's qualia at the deliberative moment itself, but looks ahead towards the consequences of the act, which are necessarily future, unperceived, merely foreseen and expected. Descartes takes as a starting point the evidence of what is directly perceived. I propose another path, which takes as starting point the impossibility of nonbelieving certain things despite their not being directly perceived.

We cannot nonbelieve that it makes sense to ask ourselves “What to do?”; and therefore we cannot nonbelieve in the truth of the answers we seek, which are of the form “Do such and such a thing!” Finally, if it makes sense to seek such answers, it is necessary that these answers are true under criteria or rules that may be accessible to us. If it were from the start impossible for us to determine the right answer, there would be no point in looking for it.

The mouse in the log

To give an example, let's suppose that I have built an outdoor fire and am about to add a log. I notice that there is a hole in the log and that at the bottom of the hole, a mouse is hiding. I have a second log at my disposal, but it is stained with mud and I prefer not to dirty my fingers. Therefore, I plan to put in the fire the first log, the one with the mouse.

I tell my friends about it, and I get three reactions:

1. Romain says: “It is but a mouse, hence a soulless body; we know this because we have never seen a mouse speak. So it doesn't feel anything, and if it screams when it roasts, it will be like the screeching of pieces of wood. So you must choose this log over the other. It is a choice less cruel to the mouse than it is kind to your fingers, which it will save from the dirt”51.

2. Pierre says: “The mouse has a nervous system, a brain, like us, and can therefore feel pain; she will suffer terribly if you put her in the fire. So take the other log, even if it may dirty your fingers.”

3. Édouard says: “From our own experience we each know that we can suffer, and, by analogy, we know this about other humans. But to ask how far down the scale of animal species there is still some form of sentience is gratuitous speculation; these are questions that cannot be answered and should be left to idle dreamers. So it makes no sense to ask whether the mouse can suffer. Therefore, you are right to choose this log over the other, and to keep your hands clean.”

Both Romain and Pierre accept that the sentience or non-sentience of the mouse is a fact. They also both believe that this fact is decisive for the answer to “What to do?”. Their difference lies in a disagreement about this fact itself.

Both also believe that they have reached their conclusion about the sentience or non-sentience of the mouse by reasoning, based on data. This data is factual, in the classical sense, including the absence of speech in mice, the presence of nervous tissue and so on.

Édouard, instead, concludes neither that mice are sentient nor that they are not; he believes this question to be meaningless. “Therefore,” says he, “we can act without considering that they are sentient.”.

Édouard's is a common line of argument but is actually a non-argument. Having found that a certain assertion A (”the mouse is sentient“) is meaningless, Édouard concludes that we must act as if it were false.

Yet if an assertion is meaningless, so must be its negation. The same reasoning, if valid, would imply that we must also act as if non-A were false, that is, as if A were true.

I think Édouard is right in a sense: if A is meaningless, we must act as if A were true, but also as if A were false. However, as I shall explain, it is impossible to act in a way that satisfies both conditions. It follows that, contrary to Édouard's assertion, A is not meaningless. The mouse is, or is not, sentient.

What are these meaningless assertions? I think we can say at least this: an assertion is meaningless if we can imagine it to be true or false, without the world being actually different. If A is meaningless, a world where A is true and another where A is false are the same world. Normal assertions, those that do have a meaning, I will call instead “substantive assertions”.

Suppose that a meaningless assertion implies a substantive assertion. One might object that this cannot happen. Yet Édouard, like Romain and Pierre, accepts that if the mouse were sentient, she should not be burned; his argument is that it is meaningless to say that she is sentient, and hence she may be burned. So he accepts that A (”the mouse is sentient“) implies B (”the mouse should not be burned“) while believing that A is meaningless and that we cannot, therefore, conclude B.

However, if we accept that prescriptive assertions are meaningful, and are therefore substantive, then the prescriptive assertion B (”you must not burn the mouse“) is substantive.

If A is meaningless, we can imagine it as false, or true, without really changing the world. But in the ”version“ of the world where A is true, we must also assume B to be true, since A ⇒ B. In the other ”version“ of the world, where A is false, B must also be true, since it is actually the same world and B is a substantive assertion.

In sum, if a meaningless assertion implies a substantive assertion, the latter is necessarily true.

As already noted, if A is meaningless, so is non-A. Therefore, we can say:

Any substantive conclusion that would follow either from the truth or the falsity of a meaningless assertion is true.

In this case, however, we have A ⇒ B, but also non-A ⇒ non-B; we must conclude that B is both true and false, that is, that we both must not and must burn the mouse. If we believe that prescriptive assertions are substantive, we cannot accept such a contradiction. It follows that our hypothesis cannot be true: it cannot be true that A is meaningless. The fact that the mouse is or is not sentient is therefore a substantive fact, a real fact of the world.

This applies to mice, but also, of course, to any other animal; indeed, to any material system enclosed in the log. It makes sense to ask whether the bacteria, wood or stones embedded in the log are sentient; the answer may be that they are not, but it cannot be that the question is meaningless.

Selfishness and non-hedonism

To reach this conclusion, I assumed that the correct answer to the question ”What to do?“ depends on the eventual pleasure or suffering that our choice may cause. More precisely, I assumed that it depends on the pleasure and suffering that it may cause to the mouse. However, there could be two other possibilities:

— the correct answer depends only on my eventual pleasure or suffering (egoistic hypothesis);

— the correct answer does not depend on anyone's pleasure or suffering (non-hedonistic hypothesis52).

Let us first consider the egoistic hypothesis. As already noted, the ”myself“ for whom this ethic tells me to care is necessarily a future ”myself“. If we repeat our ”mouse“ reasoning with this future self in place of the mouse, we come to the same conclusion: it makes sense to accept the existence of a sentience that is in fact alien to me. For this is the case of my future self: a sentience that I do not experience, nor have ever experienced, the existence of which I do not observe any more than I observe the sentience of others.

The only argument I know of in favour of solipsism is the problematic nature of otherness, of the existence of a sentience other than mine. By definition, a sentience is felt; how can I believe in the existence of a sentience that I do not feel? But this reasoning cannot stop here, since it also applies to my own future sentience. If the problem we have with otherness leads us to solipsism, it must lead us to instant solipsism, which views as non-existent any sentience other than my own present one.

But this is precisely a conclusion that we must reject if we accept that there is necessarily a right answer to the question “What to do?” and that this answer depends on some consequent pleasure or suffering – be these only “my” future pleasure or suffering. Therefore, instant solipsism cannot be correct. Despite its problematic nature, otherness exists, and this conclusion takes away its main foundation from solipsism in general.

The same can be said of the logic behind the frequently stated thesis of the radical impossibility of authentic altruism, loosely expressed by the question: “What on earth can someone else's suffering do to me?”. The answer, of course, is “nothing”, except insofar as this suffering may affect my own well-being, in which case we are back to the egoistic motivation. However, the same question arises about any concern for my own suffering: what on earth can my suffering of tomorrow (or of in five minutes) do to me now? The answer, again, is “nothing”, this time an absolute “nothing” since an effect cannot precede its cause. This logic, which is supposed to justify egoism (and even to make altruism impossible), would imply that nothing can be a true motivation for my choices; and we cannot believe this.

Conversely, the fact that our current sentience has no direct perception of our future sentience means that this future sentience of ours is in the same relationship with our present sentience as is the future sentience of any other individual: a relationship of complete otherness. If, despite this otherness, our future pleasure and pain are a valid motivation for our present choices, there is no reason why the same should not be true of the future pleasure and pain of others.

I don't claim to have rigorously disproven the egoistic hypothesis, but only to have removed the reasons to believe it, and shown that, even if it was true, it would not fundamentally change my conclusion: that it makes sense to accept the objective existence of a sentience other than that which we perceive at the moment we deliberate.

Lastly, we have to consider the non-hedonistic hypothesis, which is that the correct motivation for my actions may not depend on anyone's pleasure or suffering at all. Let us note that this is a hypothesis that we do not actually believe and that no one has probably ever believed. It would mean that pain is not a valid motivation to try to make it stop; that the suffering we experience if we hold our breath is in no way a valid motivation to continue breathing. Yet pleasure and suffering as a motivation is the reason why we protect ourselves from pain ever since we were born and why, certainly, our ancestors have been doing so for millions of years, as have all sentient beings. A belief in the non-hedonistic hypothesis would not necessarily imply that we would stop breathing53; breathing could continue to be the right act for other reasons. But this would be coincidental; believing in this hypothesis would imply being prepared to stop breathing if these other reasons vanished, regardless of the suffering of asphyxiation, which would count for nothing as a motivation.

In saying this, I have neither proven that pain and pleasure are the right motivations for our actions, nor that this is an assertion that we cannot nonbelieve. But perhaps we can take the problem in reverse. We have seen that we cannot nonbelieve that the question “What to do?” has a meaning and that the search for the right answer has a meaning, and finally that the criteria and rules for determining this answer cannot be by nature beyond our reach. There must therefore be something that can be a goal for our actions. This something must also appear to us as a goal in itself, rather than as a means to another end. And this is precisely how suffering and pleasure appear to us: as things to be avoided or sought immediately.

It would not be right to attempt to define suffering and pleasure as our immediate negative and positive ends; this would be giving a form of operational definition to objects that exist in themselves. Rather, the reasoning is that on the one hand, there must be something like a primary motivation, and on the other hand we observe that suffering and pleasure are such a primary motivation.

It is worth recalling here that the suffering and pleasure that we experience at a certain moment are not the motivation that guides our deliberation at that exact moment since the latter can produce an effect only on future suffering and pleasure. Instead, they constitute a “sample” of that future suffering and pleasure; they make them known to us. It is also true that we have direct knowledge of our immediate sentience; but if that were all there was to it, nothing would prevent us from retreating into instant solipsism. It is the deliberative situation from which we cannot escape that implies that we step outside our immediate selves, that we recognise the at least possible existence of other sentiences, and also, that we believe it possible for us to determine if they indeed exist and, if so, have an effect upon them.

It is thus the deliberative situation that implies that we have to believe in an “external” world, that is, in an objective reality. Within this reality there are necessarily causal, “mechanical” relations, without which we would have no possibility of acting; and there are also, as equally objective entities, subjectivities, connected in some way to the “material”, “mechanical” world, without which we could not know them and have an effect on them. Or better: these subjectivities are part of the “material” world, are part of the same physical world, even if we do not yet know exactly how to locate them and how to understand their interactions with the rest of the physical world.

Sentience and the deliberative situation

I have argued that we find ourselves in the deliberative situation and that this makes us ethical beings (moral agents), and free beings (endowed with free will). We are also sentient beings. Can we say that every sentient being is in the deliberative situation, and conversely that every being in the deliberative situation is sentient?

Based on the above developments, I think it is very plausible to say that every deliberative being must also be sentient. Believing does seem to be a feeling. Moreover, deliberation implies a primary motivation; we have seen that it is suffering and pleasure that play this role for us. If something else played this role in another being – say, zuffering and bleasure – it seems that it should make no difference to its behaviour; it would beg us to preserve it from zuffering, and/or to grant it bleasure, without perhaps even perceiving these “things” (if he deliberative but not sentient). We would find ourselves in the situation of the radical impossibility of determining the sentient character of being, a radical impossibility that we cannot believe in.

I believe that the converse is also likely. It appears that suffering always has the value of a primary motivation to make it stop and that the existence of such a motivation only makes sense if it is part of a deliberative process.

One could imagine a sentience that does not perceive any suffering or pleasure; that perceives only neutral qualia, such as colours, textures and sounds which give it neither pleasure nor displeasure. It would be aware of reality but would have no motivation to deliberate or to act. It seems to me, however, that knowledge of reality only makes sense to us through our possibilities of acting upon it; the situation described may be temporarily possible, but I doubt that it corresponds to a lasting state in which any real being would find itself.

It should not be believed, however, that it is possible to establish a simple, quantitative and reliable relationship between a being's capacity for action and its degree of sentience. We can be paralysed – under the effect of certain substances, for example, or in a nightmare – and still experience intense suffering. This does not imply that we do not deliberate; it just means that our deliberation does not actually lead to anything.

Nevertheless, I think that very generally sentient beings – even insects and earthworms, if they are sentient – are in the deliberative situation, and therefore are ethical agents, at least in a minimal sense.

8. Reality and Virtuality

Our technophilic culture tends increasingly to spread, as obvious, the notion of a purely logical nature of reality, and of the equivalence between the virtual and the real. I have mentioned (section 5) the myth of the thinking robot predicted by Turing. A more modern example is the Matrix film series, where the characters (If I have understood the plot correctly) cannot themselves determine whether they are real or merely the result of the execution of some sub-program in a giant computer. Yet they suffer, desire and struggle. The assumption is that since any reality can be simulated by a program – and modern achievements are often strikingly successful in simulating landscapes, aeroplanes, textures and so on – subjective perception itself can be simulated, and thus becomes quasi-real, indistinguishable from real subjectivity.

Is “virtual suffering” really equivalent to real suffering? Does it hurt?

I believe the answer is both yes and no: yes, in the sense that any existing virtual suffering would indeed be equivalent to real suffering, because we must reject epiphenomenalism (section 5). It would be equivalent in an ethical sense: we would have the same moral obligation to make it cease. But this would lead us, as we shall see, to an absurd situation. Therefore, virtual suffering cannot exist.

But what are these “virtual” things? We have seen (section 5) that in the Laplacian perspective, the totality of the world can at any moment be described by a set of numbers, and that its evolution, starting from this description, is subject to a computable determinism, that is can be predicted by the application of an algorithm. This is true of the world as a whole, at least in theory; it is also true of any part of the world. If I know at a time t₁ the complete state of a human being, which would mean, to use our billiard ball model, knowing the position and speed of each of the billiard balls that make up that human being, I can calculate what state the human being will be in (or was in) at any other time t₂, provided that I add one more piece of information: I also need to know all the external influences that may have affected the system in the time interval [t₁, t₂]. In the case of a human being, I must know all the verbal or other interactions he may have had with other humans, all the things he saw and so on; but it is not enough for me to know their general content, I must know these interactions molecule by molecule, billiard ball by billiard ball.

Given these conditions, which are implausible for a system as complex as a human being but can be fulfilled in principle, the calculation that will allow us to know the state of the system at t₂ from its state at t₁ will be a simulation. The computer will initially contain in its memory a binary representation of each of the numbers describing the system; this set of binary representations will form a model of the simulated system. The calculation will be carried out step by step, by applying the laws of evolution over very short time intervals; the shorter these are, the greater the precision of the calculation. At each step, therefore, the model will be the representation of the system at a certain instant; after a certain number of steps, it will represent the system at t₂.

This procedure is a simulation of the real system by virtue of there being a correspondence between each part of the real system and a counterpart in the model. Each billiard ball has a set of six numerical representations, describing its three positional parameters and three velocity parameters. Any set of billiard balls also corresponds to a set of numerical representations; any relationship between billiard balls corresponds to a relationship between numerical representations. The elementary time intervals of the real system correspond to the calculation steps that make the model evolve. In short, any characteristic of the real system has its “virtual” correspondent within the model that simulates it; and this remains true when it is a non-instantaneous feature, relating states of the system at different times.

If the world is Laplacian, sentience is necessarily the product of certain relationships between the “billiard balls” – molecules, fields, etc. – inside our brain. If our brain is simulated by a model as we have described it, which is always possible in principle (if the world is Laplacian), this sentience too has its virtual correspondent within this model. If the human being suffers, the model “experiences” at the “same moment” (at the corresponding stage in the algorithm's progress) a “virtual suffering”.

This is the notion of virtual suffering. We have asked ourselves whether such suffering is equivalent to real suffering; we can rephrase this question, in line with the characterisation of suffering introduced in section 7: does such virtual suffering constitute a primary motivation in our deliberations? Do we have a moral obligation to make it stop?

Penrose's positions A, B, C and D

Penrose distinguishes the following four positions concerning the physical status of sentience:

A: All thought is algorithmic; in particular, the sensations of conscious perception arise from the mere act of executing the appropriate algorithm.

B: Consciousness is a property of the physical processes of the brain; but although any physical process can be algorithmically simulated, an algorithmic simulation cannot by itself bring about consciousness.

C: Some specific physical actions in the brain produce consciousness, but these actions cannot be simulated by an algorithm.

D: Consciousness cannot be explained in physical or algorithmic terms or in any scientific way.

D is the mystical position; I think we can leave it aside since it implies outright the impossibility of determining by physical means – the only ones available to us – whether a given object is or is not conscious, and thus the impossibility of finding an answer to the question “What to do?”.

In a Laplacian worldview, our choice is between positions A and B. Both accept that an algorithmic simulation of our brain is possible, a consequence that follows from the Laplacian vision, as we have seen. They differ in the answers they give to our question about the equivalence between virtual and real suffering; A answers positively, B negatively. A is the so-called “strong artificial intelligence” position; it is the one implicitly embraced by Turing (see section 5). B by contrast represents the “weak artificial intelligence” position, and rejects the operationalist position on subjectivity, both as a definition and as a criterion. It assumes that a computer can exist that would fully pass the Turing test, without being truly sentient.

Position C rejects the Laplacian paradigm. It is the position held by Penrose, who argues for the possibility of a non-computable determinism (see Section 5). It is also the position that I defend in this article.

I explained in Section 6 why I believe Laplacian determinism to be incompatible with the deliberative situation. Penrose gives other arguments against computable determinism, based on Gödel's theorem, which I will quickly summarise. I will add a specific argument against position A, which is in line with some of Penrose's and Searle's remarks, and which has to do with the arbitrariness of the relationship between the model and the system it simulates. Finally, I will argue against position B because it appears to imply epiphenomenalism.

The conclusion will be that it is impossible to simulate algorithmically at least some physical phenomena. Finally, I will argue that it seems likely that such physical phenomena are not simulatable either algorithmically or in any other way; that is, that it is not possible, in general, to take a complete copy of a physical system.

Penrose's argument

Penrose develops in the two books I have cited a specific argument against the possibility of simulating the human capacities for mathematical thinking. He does so based on a modified form of Gödel's theorem. I refer to these books for a full exposition of his arguments and for the answers he gives to a large number of objections that have been made. I will limit myself to a brief outline.

Gödel's famous theorem (1931) concerns the possibility of a complete formalisation of mathematical reasoning. His theorem concludes that such a formalisation is not possible. Penrose uses a variant of this theorem in algorithmic terms.

The human brain is capable of proving mathematical theorems. If the world is Laplacian, everything that happens in it can be simulated by an algorithm. This algorithm will then be a theorem-proving algorithm.

What does this mean? We will assume that we can give the following characterisation. A theorem proving algorithm A will be such that:

— A operates on a countably infinite class of mathematical problems. This can be a class indexed by a natural number. An example of such a class might be: “Is there a prime number greater than the number n? Algorithm A takes as input the number n, and either eventually reaches a final state and gives us an answer (in our example: either “yes” or “no”), or keeps calculating forever without reaching a final state and giving an answer.

— We know from our mathematical insight that A is sound, in the sense that when it does give us an answer, that answer is always correct. We do not require that it always give us an answer. To take the previous example, it could be the following algorithm, described in plain language: ”test whether n + 1 is prime; if so, answer “yes”; if not, test the next number, and so on“. Because of the structure of this algorithm, we can see that if it answers us, the answer will necessarily be correct. In general, it will be our mathematical understanding of the structure of A that allows us to see (i.e. prove) that A is sound.

Penrose then considers the case where algorithm A acts on a very general class of mathematical problems, each of which is of the form: ”Take as an input an algorithm and a number; does this algorithm, applied to this number, lead to a final state or instead go on forever?”. Thus the input of A is an ordered pair (G, n), with G an algorithm and n a number, this ordered pair being itself encoded as a number.

By applying a modified form of Gödel's theorem (due to Turing), Penrose shows54 that we can determine a certain algorithm G and a certain number n such that we can prove that G applied to n leads to a final state, but which is such that A does not terminate, and hence gives no answer, concerning the pair (G, n).

Penrose concludes that such an algorithm A cannot encompass the entire human capacity to solve this class of problems, or that if it does, we cannot know it, or know that it is sound. For if we know this, and know that A is sound, we can immediately construct the algorithm G for which we know the answer, but for which A cannot give the answer.

This last conclusion itself follows directly from Gödel's theorem and is undisputed55. What is disputed – by proponents of strong artificial intelligence, in particular – is Penrose's willingness to conclude that no algorithm A can encompass the whole of our mathematical understanding. The objection to Penrose's reasoning is that our mathematical understanding may well be encompassed by such an algorithm, without that algorithm being known (by us) to be sound; and that it is, indeed, not sound. We know that humans can make mistakes, including in their mathematical reasoning.

It is not without consequences, however, to accept that human mathematical understanding can be wrong, not simply because of our distraction, but in principle. This implies that there must be some theorem that contains a reasoning error, but which is otherwise such that we are unable, even in principle (through the application of the algorithm on which our general mathematical reasoning is based), to perceive this error; we will declare the result stated by this theorem to be true, with certainty, while it is false. Penrose notes56 :

But is it really plausible that our unassailable mathematical beliefs might rest on an unsound system – so unsound, indeed, that “1 = 2” is in principle part of those beliefs? Surely, if our mathematical reasoning cannot be trusted, then none of our reasoning about the workings of the world can be trusted. For mathematical reasoning forms an essential part of all of our scientific understanding.

Penrose's argument57 thus ends with a rhetorical question to which he suggests that we answer negatively, without, however, offering a rigorous justification. I believe this argument to be correct in its substance, and capable of being more solidly grounded on the necessity of taking the internal view seriously, the very necessity that has served as my guiding thread throughout this article and which I believe is implicit in many of Penrose's own reasonings. I will not develop this point further here, for lack of space and time.

It serves to note, however, that what seems to be at stake in this whole line of reasoning is the substantive character of mathematical understanding. The “theorem proving” algorithm does not prove, or even assert, anything by itself; it only proves theorems because our independent mathematical judgement perceives it, through examination of its structure, to be sound. Whenever we do mathematics, we cannot but believe that our mathematical understanding is that of a truth independent of our assertions; if we assume that it is really no more than the execution of an algorithm, hence of a process incapable, by itself, of asserting anything about truth, our whole mathematical understanding loses all meaning. I don't think it is really possible, therefore, for us to believe that our mathematical perceptions result from the execution of an algorithm.

What I find remarkable about Penrose's approach is that it draws on mathematical understanding, a faculty often perceived as the epitome of human rationality, to support the substantive character of all understanding. The mathematician and the earthworm are put fundamentally on the same level. Both perceive, understand and participate in essentially the same situation in the world.

Penrose says little about ethics. The animal question is, however, present in his writings; he is careful to note, in each of the two books I have cited, that he does not believe that sentience is limited to the human species58, and seems open to some ethical consequences.

Algorithmics and counterfactuality

I will now approach this issue of the relationship between algorithms and sentience from another side, that of the abstract nature of algorithms. Penrose devotes several pages to this question59 in connection with John Searle's argument on the “Chinese room”60. I will develop this theme here in my way.

Position A implies that the mere execution of an algorithm can induce subjective sensations. The sensations produced are real, not just appearances of sensations; in other words, the machine (driven by the results of the calculation) would not just behave “as if” it were sentient, without being so (which would be position B).

However, an algorithm is itself a mere abstract mathematical object; as such, it has no location in time or space. How then can it give rise to a feeling, which is a real physical object?

Actually, A does not imply that the algorithm itself gives rise to feelings; it is the execution of the algorithm that is said to have this effect61. So the question arises: what counts as the execution of an algorithm?

The typical case of the execution of an algorithm is that done on a computer. The algorithm is represented in the computer's memory as a program, in the form of voltages and electrical charges; so too is the data on which the algorithm operates, forming a physical representation of our model of reality.

Through the laws of physics governing the electrical circuits that make up the computer, this data will be modified step by step in the manner specified by the algorithm. It is this physical process that constitutes the execution of the algorithm.

It is perfectly possible, however, to view the same physical process in another way: as the meaningless playing out of the laws of electronics, or the colliding of billiard balls, which, starting from a certain initial configuration, evolve after a certain time into another configuration. To see this evolution as the execution of an algorithm it is necessary to add a meaning to this physical process.

This additional meaning is first of all that which allows a certain configuration of electrical charges to represent the model, that is, to represent numbers. But it is we who establish this relationship! The usual representation of a number in a computer is by a series of electronic circuits capable of taking on two stable states. We call one of these states “0” and the other “1”. We agree that a certain collection of, say, 64 of these binary memories sometimes scattered all around the computer represents, in an order also established by convention, the binary representation of a certain number among those that form the model.

In short, the contents of the computer, without the arbitrary conventions we establish, represent nothing at all. This is in contradiction with the real, unconventional nature of the suffering and pleasure that the execution of the algorithm is expected to evoke.

It might be objected that it is the program itself that “forces” a certain interpretation of the computer's memory states in terms of numbers. For example, when adding two numbers, the binary carry is propagated in a certain order between the different binary memories; it is this order that sets the interpretation of these binary memories as numbers.

I don't think this objection is enough. Perhaps the program can make one interpretation the most “reasonable” one. Other interpretations always remain possible. We can interpret the collection of 64 binary memories in any order, even if the operation performed on these numbers is uninteresting to us. The execution process may then not be the representation of any physical process; it will however still be the execution of an algorithm, albeit not be the initial algorithm we wanted to run, but another, useless one. The problem of the arbitrariness of the relationship between the representation and the represented number is not solved.

The same can be said of the status of the program, also encoded in binary memories, and expected to represent the algorithm. But there is another issue concerning this representation of the algorithm. The effective execution, which is said to induce feelings, necessarily takes place on one set of initial data. In contrast, an algorithm, as an abstract mathematical object, is capable of operating on a plurality of sets of initial data; indeed, in principle, on an infinity of sets. For example, the algorithm for adding two numbers in some representation can add any pair from all the possible pairs of integers. It is this infinity of possible values for the initial data that makes the algorithm the representation of a certain logic. An algorithm capable only of adding two and two can be simply the instruction “print four”; nothing makes it an adding algorithm rather than a multiplication algorithm also limited to the same data; it does not incorporate any adding logic. Any algorithm capable of operating only on a finite set of data is equivalent to a finite enumeration of the results of that operation, an enumeration that does not incorporate any general logic.

Now, as I said, the concrete execution of an algorithm on a computer starts with a single set of initial data. One may say: yes, but this execution is done according to laws of physics which determine what it would do on any set of initial data; it is these laws which determine that the program as represented in memory is a representation of the algorithm.

So we are back to the problem of counterfactuality: the concrete process is the execution of the algorithm by virtue, not of itself, but of what would also happen in worlds other than the real world!

To make this problem more striking, let us imagine a computer running a certain algorithm on a certain set of initial data D. Assume that this algorithm and this data are such that this execution generates, by virtue of A, certain sensations. Assume a second identical computer, running the same algorithm on the same set of data D, except that we have added a small external device that examines the data entering the microprocessor, and a hot plate underneath. This external device is set up in such a way that if it saw other values than those in D entering the microprocessor, it would turn on the hot plate, which would melt the microprocessor. It would do so in a world other than the real world; in the real world, it does not interfere with the execution of the algorithm.

However, because the complete computer + external device system could not execute the algorithm on any other data than D, it no longer actually executes the algorithm. Therefore, because of an external device that does not interfere in any way with what is happening in the computer (since it is not triggered), this second computer no longer generates the sensations that the first one did.

This implies that the fact that a certain setup generates certain sensations depends not only on what happens in the real world, but also on what would happen in worlds other than the real world...

This is just one of the astonishing, and indeed non-credible, consequences of the abstract nature of an algorithm and the arbitrary nature of the correspondence between the representation of data in a machine and the data itself. Without going into detail, the following assertion seems likely: in a Laplacian world, any physical process whatever, at any moment whatever can, given the right mapping rules, represent the execution of any algorithm whatever on any data set whatever. It would follow that, depending on the correspondence rules we choose to consider, suffering and pleasure, as well as any sensation, would be everywhere, at every moment.

It thus appears clearly that if A were true, the purpose of reducing suffering and increasing pleasure could make no sense. This would render meaningless the deliberative situation, to which however we cannot fail to attach meaning. Therefore, we cannot believe that A is true.

Position B and epiphenomenalism

Position B also accepts the Laplacian framework, and thus assumes that the algorithmic simulation of any phenomenon is possible, and, in particular, that of the entire brain of a sentient being. It postulates, however, contrary to A, that such a simulation would not generate the sensations of which the simulated system is the seat. Sentience, according to B, is not linked to the execution of an algorithm, but to this execution within a certain type of matter.

This is Searle's position, but he does not explain what this link might be. The advantage of this thesis is that it does not view sentience as derived from an algorithm, hence from an abstract object, but from the concrete object within which the algorithm is executed. The computer simulation of a hurricane, tells us Penrose (following Searle), is certainly not itself a hurricane62.

This position appears to imply epiphenomenalism (which I defined in section 5) quite directly, and should therefore be rejected. Indeed, sentience is present in the simulated system, but absent in the simulating system. The result of the evolution of the simulating system cannot, therefore, be caused by sentience. For example, let us assume that the computer simulating a human being is placed within the skull of a humanoid robot and that as a result of the execution of its algorithm, it activates the motor organs of the robot, giving it the same behaviour as the simulated human being. If the human being screams in pain, the android will scream, but with no pain; despite this, the scream will be the same. In the human being, unless we assume the epiphenomenalist thesis to be true, pain is the cause of the cry; at least, it participates in its determination. In the android, no pain is the cause of the cry. The latter will be entirely determined by the execution of the algorithm on the data modelling the human brain; the causal relationship between the cry and this data is the same as the causal relationship between the human cry and the parameters represented by this data within its brain, namely the position and speed of the various billiard balls. The pain, absent in the android, seems superfluous in the human being and appears to come in addition to an already complete causal relationship; there is nothing left for it to cause. This is the epiphenomenal situation.

Can all physical systems be simulated?

The conclusion is that a sentient physical system cannot be simulated algorithmically; for we have argued against A that such a simulation cannot be sentient, and against B that instead it must be.

If this conclusion is true, it implies that physics cannot be Laplacian.

Penrose speculatively seeks to develop a non-Laplacian physics, where a non-computable determinism would come into play. One can imagine that within such a physics, the simulation of one system by another would remain possible, provided that the system simulating a non-computable system evolves itself non-computationally; in particular, the simulating system could not be a computer.

In section 6 I showed that the possibility of simulating a sentient being led to a contradiction, in particular in the context of Newcomb's paradox. I had assumed that this simulation would be done by computer; in reality, however, the algorithmic character of the simulation played no role. My conclusion, if valid, implies the impossibility of any simulation of a sentient being.

My reasoning about Newcomb's paradox was related to the impossibility of not believing in our own free will. It appears that the problem we have with the very definition of free will is at least partly due to the ingrained and largely unconscious habit we have of assuming that any physical system can, necessarily, be simulated by another. If we accept that this is not the case, we may retain determinism – at least some form of non-computable determinism – without it remaining possible to acquire at a given moment all the information defining a system in order to “replay” its evolution elsewhere. Our free decisions could retain their uniqueness and unpredictability, while nonetheless being determined.

It is remarkable that this conclusion also “rings a bell” for anyone familiar with the structure of quantum mechanics. This is because quantum mechanics also makes it impossible, in general, to measure a system completely and reproduce it identically without destroying the original system. As I mentioned at the end of section 6, I am not saying that quantum mechanics as it exists is the solution to our problem, but I see this convergence as a sign that we may well be on the right track.

9. Some Tentative Conclusions

This is by far the longest article I have written, and the one that cost me the most effort. The main difficulty has been the impression that I was tackling a little-recognised field, particularly in France, and had to face contradictory but strongly held convictions, which implied developing considerations that do not fit into any established discursive register. Activists usually prefer ideas that are immediately effective. Philosophers typically know little about physics, which they presume to be irrelevant to their field. Physicists, symmetrically, look down on all philosophy, especially if it claims to have implications for their domain. I have had to defend a point of view that contrasts with the orthodoxy of each of these fields, because of its ethical realism, and also, paradoxically, because of its physical realism.

I would never have developed these reflections if I had not discovered, three years ago, the works of Roger Penrose; and if the team of the Cahiers antispécistes had not given its active and patient support to the project of a thematic issue on this subject. One of my greatest fears was, and remains, the charge of “mysticism” that will inevitably be launched at my theses. I believe it is useful to explain below why I see such a qualification as unfounded.

First, however, I would like to round up a few practical conclusions that I think can already be drawn from the theses I have developed; conclusions that I believe can be grounded only in considerations that break with the dominant physical and philosophical conceptions.

Sentience: what criteria?

Admittedly, the criteria of sentience that can be derived from my thesis are not far from those that are suggested by intuition. What then is the practical point of all these developments? It lies, as argued in section 1, in the hope of better grounding these criteria. For we only listen to our intuition if we choose to; we have seen that large sectors of the population prefer not to, moving back and forth between a convenient attribution of sentience to carrots or even to stones – declaring that anything can be said, hence nothing can be concluded – and an equally convenient restriction of sentience to the human species alone.

Merely managing to talk about sentience without feeling that any discussion of it must necessarily lead to a scientific dead end or to dissolving it into a functionalism dependent either on the arbitrariness of human descriptions or on a natural teleology – both unlikely to ground serious ethical consideration – seems apt to lend strength to our discourse when we say that yes, pigs and hens are sentient, and no, carrots are plausibly not, and finally, if we do not know today if and to what extent insects are sentient, we may know someday and that at least the question has a meaning since it has an ethical one.

A first criterion we can put forward is that of intelligence. I believe that intelligence – the capacity to understand the world – is necessarily linked, at least at the evolutionary level, to sentience. This statement is both consistent with our intuition and surprising in light of the usual views of anti-speciesism. Does a more intelligent being deserve more consideration for its interests? Certainly not; it is sentience, not intelligence, that justifies taking a being's interests into account; or more precisely, that makes a being have interests to take into account. However, it is not contradictory with this position to affirm that a link exists between intelligence and sensibility.

Intelligence, the ability to understand the world, is not a specific human characteristic. It is a necessary ingredient of the deliberative situation. If decisions could be made by a three-neuron drive comparator, there would be no need for suffering or pleasure, for deliberation or for understanding the world. I believe that the deliberative situation involves non-algorithmic mechanisms, the outcome of which cannot be predicted “mechanically”. Indeed, it is the debate about whether or not animals are “mechanical” that has historically been, and still is in many discourses, tantamount to deciding if they are sentient. If they are mere machines, Descartes told us, then they do not feel; their cries are not caused by suffering and by an attempt to act on the world to put an end to this suffering, but only by the inexorable, infinitely reproducible and predictable course of a clockwork mechanism. Conversely, the ability to “innovate” seems a specific feature of the deliberative situation; and we have seen that this most likely involves sentience.

A certain discourse on plants tends to attribute sentience to them simply because they sometimes react to grazing by “telling” other plants, through the production of a certain gas (ethylene), that they need to protect themselves. This “communication” can be explained by entirely automatic mechanisms that never involve a deliberative situation; it cannot, therefore, be seen as an indication of sentience.

A system may certainly be more or less intelligent; I believe the same holds for sentience. However, it is not obvious that the correlation between intelligence and sentience is direct or constant. Moreover, in the absence of a clearer understanding of both intelligence and sentience, we have no accurate way of measuring either. It doesn't appear absurd, however, to assume that a fly may be sentient, but less so than an adult human or elephant.

Concerning this question of the possibility of “more” or “less” sentience, we will have to admit that our consciousness is not an indivisible whole; or that it is less so than we tend to think. Cases of “split brain” – where the communication between the two hemispheres of the brain has been cut – suggest that it may be possible, for example, for one hemisphere to be happy and the other sad. If the suffering of the whole – of both hemispheres together – ethically counts as 1, then the suffering of each hemisphere must count as 1/2. In any event, we can hope one day to quantify suffering and happiness when we better understand these phenomena. Again, however, we must beware of simplistic conclusions that would have that a larger brain must suffer more than a smaller one!

Another feature probably correlated with intelligence and the existence of deliberative situations in general, and therefore with sentience, is the organism's capacity for action. A plant can do nothing against a predator; if it suffered at every bite, this suffering would be in vain. It would urge the plant to deliberate, but this deliberation could never lead anywhere. It is worth noting that deliberation, in the only beings that we know deliberate – in animals, therefore, in their nervous tissue – is a great consumer of energy, of that very energy which is very generally, for life, the limiting factor. Using the “brain muscles” is tiring, and we avoid doing it for no reason. One may surmise that deliberation by its nature involves a great deal of energy consumption. Evolution is unlikely to develop such a phenomenon if it did not increase survival and reproduction.

Evolutionary reasoning cannot be absolute, however. A characteristic may well remain in an organism after it has become useless or even harmful. I have in mind, for example, mussels and oysters (bivalves); they have nervous tissue and belong to a phylum (molluscs) of which some members (octopuses, etc.) are certainly sentient and highly intelligent. In bivalves, sentience may be useless; their capacity for action seems to be limited to the opening and closing of their shells according to simple external factors (immersion, temperature...). However, one may imagine that in their case sentience has not regressed to the point of disappearing.

I think it is indeed interesting to consider sentience in the context of evolution. Suffering, it is often said, is “merely” a mechanism invented by evolution to elicit avoidance behaviour, for example. A certain view of Darwinism, known as adaptationism, ultimately reduces all features of an organism to their function alone, regardless of their conditions of possibility. However, wings on birds are not reducible to their utility for escaping predators; their existence involves also specifically physical phenomena, such as the lift they obtain from the air without which flight would not be possible. If the air were less massive, for example, the wings would have to be larger to do the same job; their development might not have been “worth it” in evolutionary terms.

Suffering and pleasure clearly are mechanisms that increase the survival and reproduction of organisms! I propose, however, that sentience, as well as intelligence – the possibility of non-algorithmically determined deliberation – may have represented, somewhat like flight, possibilities offered by physics; evolutionary mechanisms would have “taken advantage” of these possibilities while remaining dependent on the physics that underlies them. Sentience and deliberation are therefore not “mere” mechanisms set up by evolution, but physical phenomena in their own right, with their specific constraints.

One such constraint may be the energy cost, which I have noted. Another is the sluggishness of our thoughts. This is not a characteristic of nervous tissue in general; consider the speed with which we integrate the mass of visual information representing a face or a landscape and recognise its elements almost instantly. But these are automatic, unconscious operations. In contrast, as soon as we try to understand the meaning of even a simple sentence that presents some novelty – for example, an unfamiliar mathematical assertion – it takes us seconds, even sometimes weeks. We understand and think slowly. If it were possible for us to do the same much faster, we can assume that evolution would have found the way.

This lack of speed may be related to Penrose's reflections on certain structures within certain nerve cells, which may be the sites of quantum phenomena requiring a certain minimum amount of time. These reflections also appear to suggest that it is indeed certain kinds of tissue, and not others, that can be the seat of sentience; the obvious candidate being, of course, nervous tissue. It is certainly not the case that all nervous tissue is the seat of sentience; it may well be true, however, that only this tissue, and possibly others possessing similar structures, can be sentient.

Are these considerations mystical?

If it is mystical to consider questions that we do not know how to answer, I accept that my theses here are mystical. I should note, however, that I am not at all asserting the impossibility of ever answering these questions; on the contrary, my efforts have been aimed at ceasing to view sentience as supernatural and at starting to create conditions for grasping it within a unified understanding of the world.

If I had been content with setting out, on the one hand, the tenets of modern physics, which actually deny the very possibility of believing in the reality of both stones and feelings, and on the other hand some Catholic or other set of religious convictions, I would have incurred far less the reproach of mysticism. It is true that my subject is something like “spirit”, or mind if one takes these words as synonyms for “sentience”. My “mysticism” is mainly in that I speak of mind outside the recognised frameworks which allow it to be tidily cut off from the world of stones.

Lastly, my reflections are completely devoid of one of the most common features of what is generally categorised as mysticism, namely, holism. I do not believe that “the spirit” can be gathered into a great whole. Quite the opposite: sentience appears to me rather divisible. On the other hand, a collection of sentient and deliberative beings often behaves in a quite mechanical way. There is nothing more predictable and mechanical than a crowd, in many circumstances where, despite this, each individual remains an intelligent and free being. Thus, while I believe in the reality of sentience and its potential presence in all matter, I do not believe in a great spirit of the universe, in something like a god. I do not believe that the universe is driven by a purpose. At the most, I can think that perhaps a tendency present in all sentient beings can lead them, gradually, to increasingly harmonise their interests, their actions and their desires.

More on impossible nonbeliefs

I would like to return to the principle that I have made good of repeatedly in this article, that of the “foundation by the impossibility of not believing”. I think it can help us out of some of the dead ends of philosophy and physics. However, it can also easily be perceived as a form of renunciation. If we cannot prove something, but, because of our situation, cannot nonbelieve it, we might as well accept it; in practice, it makes no difference, but we will remain dissatisfied. A higher, more idealistic part of us aspires to ground our beliefs on reason alone.

I do not think that such a view is justified. Philosophy has demanded that everything be based on reason. This is certainly a good thing when it saves us from mistakes. But, it will be said, it is not to avoid mistakes that one is a philosopher; it is out of love of reason for its own sake!

There is something of an admission here: the love of reason is not just the love of truth. Truth can have an immediate practical significance; reason, on the other hand, has a practical significance only insofar as it allows us to reach the truth. Why, then, should we be in love with reason, rather than with mere truth?

I believe that this passion for reason “for its own sake” is a way of projecting ourselves out of the world. We would like to be elsewhere, in an elsewhere of pure spirits, where nothing is corrupted and we would not die like beasts die and rot. In order not to rot, we want to be that thing without substance, that is, reason. And just as we disembody ourselves, we disembody the world, reducing it to a senseless game of billiard balls. This is the Platonic, Christian, and finally Cartesian partition of the world, that of absolute speciesism: humans and stones. And the result is that all are dead, both humans and stones.

To acknowledge that we believe what we cannot nonbelieve is not to give up; it is to accept our situation in the world, the situation that makes us exist. We think and feel, but we are mere matter, like stones, bacteria, flies and pigs. That we feel, and the stones do not, remains to be explained; but we are not of a different substance from them. We are in the world as much as they are and we make up the world as they do.

If we must love a notion, I prefer to love truth than reason; and our desire for truth is fully satisfied if we accept my principle.

Let us assume that Morganne believes proposition A to be true, and at the same time knows that she believes this. Will her desire for truth be satisfied? The answer is yes; for the conditions of satisfaction of this desire are purely subjective. Whether A is, in fact, true or false makes no difference from Morganne's point of view. Since she is certain – rightly or wrongly – that A is true, and knows this (that she is certain of a proposition she is certain is true), she can but be satisfied.

This reasoning may seem cynical; Morganne is satisfied while perhaps being wrong. But when it comes to things that we cannot nonbelieve as a result of our situation as sentient and deliberative beings, there is no such viewpoint from outside. As far as these things are concerned, neither we nor anyone else believes Morganne to be wrong. What more can we ask for?

Gwenva

Gwenva died almost a year ago. He was a cat, as can be observed in Figure 1 at the beginning of this article.

The picture shows him during a physics experiment. His fascinated look fascinates me; he is attempting to understand the world. He is convinced that he can understand something of it and that at the same time, something of it escapes him; he thinks that the world exists in itself. In this, he is right, unlike many of the founders of quantum mechanics.

He believes in the laws of physics. His paw is raised but he hesitates; he knows he is free to hit the water, or not to do it; he will perceive the result of his choice, in either case. He believes in his freedom, and he believes in causality. He also believes in the reality of the pleasure of living and learning, even for a modest non-human cat.

Gwenva the physicist believed in all those things that our physics and philosophy would have us renounce. What a clever fellow, this Gwenva!