Ce texte a été publié dans le n°23 des Cahiers antispécistes (2003).
193 min.
Résumé: L'émergence de l'animalisme, et donc de la prise au sérieux de la sentience des animaux non humains, rend intenable la division traditionnelle du monde entre nature et humanité. La sentience, autrefois vue comme l'apanage de l'espèce humaine, fait en réalité partie du monde physique; la science doit en rendre compte. Le présent article vise à énoncer quelques contraintes à laquelle devra répondre une physique sentientiste.
Ce problème – dit «problème difficile de la conscience» (hard problem of consciousness) selon l'expression de David Chalmers (1995) – a fait l'objet de nombreuse tentatives de résolution, ou encore de négation. Leur défaut commun est de n'envisager la question que sous un angle descriptif, à l'exclusion de toute considération éthique.
Or non seulement l'existence, objective, de la sentience (du «subjectif») fait intervenir de manière essentielle l'éthique, mais il en va de même de l'existence de ce qu'on appelle «monde matériel». L'éthique doit être définie, par souci de cohérence et de complétude, comme la théorie du prescriptif en général, c'est-à-dire de la réponse juste à la question «Que faire?»; elle inclut en particulier la prudence (souci de ses propres intérêts futurs). Loin d'être une particularité humaine, elle est le fait de tout être sentient, délibératif, puisqu'il doit répondre à cette question; les animaux non humains sont, comme les humains, des agents moraux.
On dit souvent que les prescriptions, contrairement aux descriptions, n'ont pas de valeur de vérité (ne sont ni vraies ni fausses). Cependant, l'examen des fondements généraux de notre connaissance fait apparaître qu'à défaut de fondements rigoureux, nous avons seulement une impossibilité de ne pas croire en l'existence du monde matériel; et que cette même impossibilité concerne l'existence des vérités prescriptives. Si la réalité du prescriptif est mal fondée, elle ne l'est pas plus que notre croyance en l'existence même du monde. De plus, ces deux impossibilités se renvoient l'une à l'autre.
La vision du monde que nous donne la physique actuelle rend son évolution équivalente à l'exécution d'un algorithme. Or l'exécution d'un algorithme n'a de réalité que conventionnelle et n'est donc pas susceptible de produire de la sentience (des qualia). Adoptant la distinction faite par Roger Penrose entre déterminisme calculable (par un algorithme) et déterminisme en général (potentiellement non calculable), et sur la base de l'impossibilité de ne pas croire en l'objectivité de la valeur de vérité des propositions prescriptives, je conclus comme Penrose que le monde physique ne peut être régi par un déterminisme calculable. La sentience apparaît comme un phénomène physique, potentiellement déterministe, mais non calculable, régi par des lois encore inconnues.
Je conclus en esquissant des critères pour la reconnaissance de la présence de la sentience dans un organisme donné.
La sensibilité*, objet central de toute éthique et de toute action, est une réalité du monde. Elle est une réalité en soi, dont l'existence ne dépend pas d'un point de vue; elle en est une réalité objective. Dans la mesure où notre cerveau est fait de matière – dans la même mesure que le sont une table ou un caillou – la sensibilité est une propriété possible de toute matière. Elle est du domaine de la physique, laquelle doit rendre compte des relations qu'elle a avec les autres éléments du monde réel, et permettre de déterminer quand, où et avec quelles caractéristiques (souffrance, plaisir et autres qualia1) elle se produit.
Pourtant, la physique d'aujourd'hui est incapable d'intégrer la sensibilité dans sa description du monde. Le problème ne se résoudrait pas par la simple découverte d'un nouveau phénomène ou d'une nouvelle loi. Nous avons besoin d'une refonte en profondeur de notre conception de la réalité et de la physique. Je n'apporterai pas ici les clés d'une telle refonte, mais me contenterai d'expliciter quelques raisons qui me la font croire nécessaire, et de proposer quelques conditions qu'elle devra satisfaire.
Mes réflexions s'inspirent pour une part importante des travaux que le mathématicien anglais Roger Penrose a exposés dans deux ouvrages disponibles en français2, dans lesquels il soutient que notre physique actuelle est incapable de rendre compte des processus mentaux. Il le fait sur la base de nos facultés de compréhension mathématique et de l'impossibilité de simuler celles-ci par l'exécution d'un algorithme; cette impossibilité découlant, selon lui, d'une application du célèbre théorème d'incomplétude de Gödel (1931). Je crois cette argumentation très importante, mais non tout à fait concluante. En filigrane dans les ouvrages de Penrose se trouve ce qui constitue mon argumentation centrale: le caractère incontournable du point de vue interne, subjectif, et le fait que ce point de vue rend impossible de se faire une théorie du monde sans attribuer au subjectif, c'est-à-dire à la sensibilité, et aussi à la vérité des propositions prescriptives et à la liberté de choix, le caractère de faits. C'est aussi sur cette base, je crois, que l'on peut confirmer la justesse des déductions de Penrose, et en particulier de son affirmation selon laquelle l'évolution du monde ne peut être entièrement soumise à un déterminisme calculable; si le monde est déterministe, il doit l'être au moins en partie d'une manière non calculable, c'est-à-dire non algorithmiquement reproductible.
Penrose s'intéresse à la pensée sous une de ses formes les plus «abstraites», et spécifiquement humaines, le raisonnement mathématique. Ce que suggèrent cependant ses travaux est bien que toute compréhension réelle – même les raisonnements les plus pratiques, présents assurément chez bien des animaux non humains – consiste nécessairement en un processus non algorithmique. La compréhension réelle implique la perception du caractère de vérité de certains faits, qu'il s'agisse de la présence d'un prédateur dans les environs ou d'un résultat mathématique; elle ne peut se ramener à l'exécution – nécessairement insensible – d'un algorithme. Je soutiendrai que la sensibilité, l'intelligence (faculté de comprendre), la liberté et l'éthique (recherche non algorithmique de la réponse vraie à la question «Que faire?») sont intimement liées, et que par conséquent tant l'intelligence que la liberté et l'éthique sont des caractéristiques de tout être sensible.

Cela permettra déjà de dégager, ou plutôt de commencer à mieux fonder, un certain nombre de critères qu'il nous paraît naturel d'adopter pour déterminer si un être donné est sensible; comme le caractère non «automatique» de son comportement ou la possession de tissus d'un certain type, à savoir les tissus nerveux. Cela permettra de comprendre la place de la sensibilité dans l'évolution. Cela permettra de fonder, comme vraies, nos obligations morales envers tout être sensible quel qu'il soit. Enfin, cela impliquera la nécessité de reconstruire nos conceptions de la réalité physique et permettra d'esquisser quelques contraintes que ces nouvelles conceptions devront satisfaire.
1. Certitudes des uns, certitudes des autres
On pourra s'étonner que j'affirme ici l'incapacité de notre physique à rendre compte de la sensibilité. De fait, ce n'est pas là la position de bon nombre de philosophes, et tout particulièrement de philosophes antispécistes. Peter Singer, par exemple, consacre huit pages dans La Libération animale3 à contrer la thèse cartésienne selon laquelle les animaux ne posséderaient aucune sensibilité, ne ressentiraient rien du tout. Il le fait sur la base d'une série d'arguments à caractère scientifique, sans se poser la question du statut scientifique de la sensibilité elle-même. Ses arguments concernent le comportement des animaux, leur possession d'un système nerveux, et l'utilité évolutionnaire de la douleur; c'est sur cette base qu'il conclut a contrario à l'absence de sensibilité chez les plantes4. On voit fréquemment mentionnée aussi la présence chez tel ou tel animal de certaines substances chimiques, telles les endorphines mentionnées par Joan Dunayer dans son article sur les poissons paru dans le numéro 1 des Cahiers antispécistes5. Mon expérience est que de façon très générale les militants antispécistes tendent à penser que le statut scientifique de la douleur et de la sensibilité pose peu de problèmes, et que notre incapacité, par exemple, à dire si une fourmi peut ou non souffrir résulte simplement de l'absence d'attention accordée par les scientifiques à la question.
Cette attitude contraste fortement avec une autre, très répandue, justement, chez les personnes de culture scientifique et qui se réclament d'un certain rationalisme. Chez elles, la tendance est au contraire de déclarer que la question de savoir si un animal donné est ou non sensible est dépourvue de sens. Erwin Schrödinger, un des fondateurs de la mécanique quantique, a formulé avec netteté cette position – qui n'était pas la sienne – dans la réponse imaginaire, mais typique d'un certain point de vue, qu'il met dans la bouche d'un «rationaliste» à qui on demanderait «quel type de processus matériel est directement associé à la conscience»6:
Un rationaliste peut être tenté de régler cette question brutalement, à peu près comme suit. D'après notre propre expérience, et par analogie lorsqu'il s'agit des animaux les plus évolués, la conscience est connectée à certains types d'événements dans de la matière organisée et vivante, c'est-à-dire à certaines fonctions nerveuses. Se demander jusqu'où, en descendant l'échelle des espèces animales, il y a encore quelque forme de conscience, se demander à quoi peut ressembler la conscience dans ses étapes précoces, relève de la spéculation gratuite; ce sont des questions auxquelles on ne peut pas apporter de réponse et qui doivent être laissées à des rêveurs désœuvrés. Il est encore plus vain de se perdre en pensées sur la possibilité que d'autres événements, des événements dans la matière inerte, sans même parler de tous les événements matériels, sont peut-être aussi, d'une façon ou d'une autre, associés à la conscience. Tout cela est fantaisie, aussi irréfutable qu'indémontrable, et n'est donc d'aucune utilité pour la connaissance.
Cette position qui se veut «rationaliste»7 déclare, comme je l'ai dit, dépourvue de sens la question de la sensibilité (conscience) animale. Elle admet par contre sans réserves «notre» sensibilité – «notre» voulant dire celle des êtres humains. Celle-ci résulterait de notre expérience, et serait donc de l'ordre des faits, ferait partie de la réalité du monde; elle serait d'ailleurs de quelque façon reliée aux «fonctions nerveuses», c'est-à-dire à des événements physiques banals, observables. Mais en dehors de l'espèce humaine – et de quelques animaux, ceux qui sont «les plus évolués» – le statut de la sensibilité change radicalement. Concernant les animaux «peu évolués», et les objets inanimés, cette position n'affirme pas leur absence de sensibilité; elle dit, plutôt, que dans leur cas la question de la sensibilité n'a pas de sens. Elle ne serait pas, dans leur cas, de l'ordre du fait.
Les attitudes des uns et des autres ont en commun de considérer la question du statut scientifique de la sensibilité animale comme un non-problème: les uns, parce qu'ils la supposent résolue, les autres parce qu'ils l'estiment dépourvue de sens. Je crois bon de briser ces deux certitudes tranquilles; et en particulier, celle de «mon camp», celle des personnes qui luttent pour le respect des intérêts des animaux. En effet, la position d'en face, celle qui domine chez les scientifiques, n'est pas sans raisons; et pour pouvoir dialoguer avec ces scientifiques, et avec l'ensemble de la société qui leur fait confiance, et répondre à leurs arguments par des arguments sincères et convaincants, nous devons reconnaître ces raisons. De façon plus générale, le réel nous appartient, autant à nous qu'à quiconque; nous ne devons pas permettre qu'au nom de la science, c'est-à-dire au nom de la réalité, on dénie l'existence ou la pertinence de la sensibilité animale. Nous devons donc prendre conscience des authentiques difficultés qu'il y a à intégrer la sensibilité dans le point de vue scientifique, et commencer à chercher des pistes de résolution.
La question a des incidences directes sur les intérêts des animaux non humains. Florence Burgat rapporte8 la tendance des chercheurs de l'INRA (Institut national de la recherche agronomique) chargés d'étudier la question du bien-être animal à estimer qu'il s'agit d'une non-question, correspondant uniquement à une «demande sociale», c'est-à-dire à une lubie d'un public mal informé (puisque par manque d'esprit scientifique il prend au sérieux l'idée qu'un animal puisse avoir un bien-être). Dès lors, le but de leurs études sera de contenter aux moindres frais cette demande jugée absurde; on mesurera le bien-être de l'animal par sa santé, critère considéré comme «objectif» et lui-même traduit en termes de courbes de croissance et autres indices très peu contraires aux intérêts des professionnels, intérêts jugés, eux, très réels. Dès lors que c'est aux scientifiques que l'on confie le soin d'étudier ce qui est, et que les scientifiques estiment que la souffrance animale n'est pas, ou – ce qui revient au même dans leur esprit – que cette question n'a pas de sens, toute prise en compte sociale sérieuse des intérêts animaux est impossible.
2. Des humains et des cailloux
La thèse centrale de cet article est en quelque sorte double, donnant à la fois tort et raison à chacune de ces deux certitudes. Elle affirme:
— le caractère incontournable du point de vue subjectif et l'impossibilité de ne pas croire au caractère de vérité réelle des assertions éthiques (prescriptives) et à la réalité objective de la sensibilité et de la liberté;
— l'impossibilité d'intégrer la sensibilité et ces autres faits dans la conception de la réalité physique qui domine les esprits encore aujourd'hui.
Ces deux impossibilités aboutissent à une contradiction, dès lors que l'on tient pour acquise cette conception de la réalité physique. Je vais revenir longuement sur chacune, mais je crois aussi qu'il en existe une conscience confuse mais diffuse et tenace dans notre culture. Les deux propositions sont rarement formulées, et la contradiction à laquelle elles mènent rarement mise en lumière. Au lieu de cela, nous faisons dans notre esprit une division du monde en deux compartiments radicalement dissemblables: nous le traitons comme s'il n'était fait que d'humains d'un côté, et de cailloux de l'autre. Les deux propositions contradictoires seront reconnues chacune comme vraie, mais séparément: l'une dans le monde des humains, l'autre dans celui des cailloux.
Reprenons la position «rationaliste» dépeinte ci-dessus par Schrödinger. Elle commence par admettre la sensibilité comme un fait chez les humains: «D'après notre propre expérience, (...) la conscience est connectée...». La conscience, donc, est de l'ordre du fait, chez les êtres humains. Ceux-ci faisant partie du monde physique, on pourrait imaginer que ce même concept de sensibilité soit applicable partout dans ce monde; non que la sensibilité soit nécessairement présente partout, mais que là où elle n'est pas présente, elle soit au moins absente. Mais ce n'est pas cela que dit cette position «rationaliste»; elle nous dit qu'au-delà des limites du monde humain9, la question même de la sensibilité relève de la «spéculation gratuite»; à ce genre de questions «on ne peut pas apporter de réponses». En dehors du monde humain, la sensibilité n'a pas de sens.
Le «rationaliste» de Schrödinger ne nie par contre pas tout à fait que les lois qui gouvernent le monde non humain puissent s'appliquer au monde humain; la sensibilité, dit-il, est connectée à certains types d'événements dans de la matière. Il ne prend cependant guère la peine de détailler cette «connexion»; et si connexion il y a, on ne voit pas pourquoi sa présence ou son absence ne resteraient pas repérables en dehors de l'espèce humaine, y compris «en descendant l'échelle des espèces animales». Il ne semble donc pas tellement persuadé de la possibilité d'établir une telle connexion. D'autres, qui se réclament moins d'un «rationalisme» intégral, feront explicitement de l'«homme» un domaine régi par d'autres déterminismes que ceux qui gouvernent la simple matière; nous sommes corps et esprit, insistent-ils. Telle était la position de Descartes, souvent considéré pourtant comme un des principaux fondateurs de la pensée rationaliste. Aujourd'hui, l'attitude affichée est souvent moins explicite, et relève plus d'une sorte de schizophrénie érigée en dogme; d'un côté on accepte intégralement les lois de la physique moderne, et de l'autre on maintient que ce qui est humain relève d'un autre ordre. C'est là typiquement l'attitude religieuse-laïque; c'est celle que promeut l'Église catholique, et qu'encore aujourd'hui elle reproche à Galilée de ne pas avoir eue, ou pas assez.
La règle générale est d'admettre par principe que l'être humain, système nerveux compris, doit forcément être soumis aux mêmes lois de la physique que le reste de l'univers; mais cette affirmation demeure vide, dépourvue de tout pouvoir opératoire. La complexité du système nerveux sert pour cela à la fois de bonne raison et d'alibi; bonne raison parce que cette complexité est réelle et rendrait impossible l'analyse détaillée, particule par particule, de tous les événements qui se déroulent dans un cerveau; mais alibi parce qu'au-delà de la pétition de principe, on ressent bien, confusément ou clairement, que la complexité ne change rien au fond, et que la sensibilité ne peut tout simplement pas résulter de cette physique qui, pour l'essentiel, décrit le monde comme un ensemble de boules de billard évoluant «mécaniquement», c'est-à-dire selon des lois d'un déterminisme calculable.
Ce partage du monde entre humains et cailloux s'étend pratiquement à la totalité de nos concepts. Au cœur de notre droit il y a la distinction entre les personnes et les choses; tout ce qui n'est pas humain est une chose, tous animaux non humains compris. Au cœur de notre philosophie, l'opposition entre culture et nature; seuls les humains relèvent de la culture, et tout le reste de la nature. Nos universités se divisent systématiquement en disciplines littéraires, qui étudient l'esprit et les «sciences humaines», et en disciplines scientifiques, dites aussi de science dure (comme les cailloux), qui étudient tout ensemble les cailloux, les choux et les hiboux. La sociologie et l'anthropologie relèvent des premières, l'éthologie des secondes, au même titre que la chimie. Entre l'être humain et l'animal, dit-on, il existe un abîme; le premier pense et décide librement, le second est mû par l'instinct comme le caillou par la pesanteur.
Les animaux: grains de sable parmi les cailloux
L'exclusion radicale, cartésienne, des animaux non humains du domaine du sensible est intimement liée à la division du monde en humains et en cailloux; et celle-ci est à son tour liée à la double impossibilité que j'ai mentionnée. La question animale est donc directement impliquée dans la levée de cette double impossibilité.
Si le monde était réellement fait de deux catégories d'objets facilement repérables, une partition conceptuelle absolue ne serait pas indéfendable. Nous pourrions considérer que certains concepts s'appliquent à une catégorie d'objets, mais non à l'autre. Ce serait le cas en particulier des concepts qui fondent notre éthique, nos diverses éthiques. Même sans définition précise les notions de sensibilité, d'autonomie, de dignité, de libre-arbitre et ainsi de suite, nous pourrions constater que tous les signes qui, spontanément, nous font penser d'un être humain qu'il possède n'importe laquelle de ces caractéristiques sont satisfaits par tous les humains et par aucun caillou. Dès lors, face à un objet quelconque du monde, nous n'aurions pas besoin d'autre critère que son appartenance ou non à la catégorie des humains pour décider s'il doit être inclus dans la sphère des patients moraux, c'est-à-dire si nous devons le prendre en compte pour lui-même dans nos décisions.
Tel est le monde tel que le pense l'humanisme, tel que le pense notre culture en général. Pourtant, le monde réel n'est pas fait ainsi, et nous le savons très bien. Déjà au sein de l'espèce humaine, tout le monde ne possède pas, au moins de façon claire, les signes dont j'ai parlé; il existe des embryons et des fœtus, des comateux, des handicapés mentaux profonds. C'est surtout le statut moral des embryons et fœtus qui fait débat, en raison de l'existence d'un enjeu pratique, et aussi d'une continuité évidente dans le développement depuis l'œuf fécondé jusqu'au nouveau-né et au-delà; s'il y a un abîme entre les choses et les personnes, c'est sans bruit et sans efforts que l'embryon semble, on ne sait trop quand, le franchir.
On parvient pourtant maladroitement à contenir cette brèche, en invoquant le fait que les êtres concernés, s'ils ne possèdent pas les caractères des humains adultes typiques, sont au moins destinés à les acquérir (dans le cas des embryons), ou les ont possédés (dans le cas des comateux); ou encore les possèdent par essence, bien que par «accident» ils ne les possèdent pas (dans le cas des handicapés mentaux profonds). La partition du monde en personnes et en choses peut subsister.
Ce sont les animaux non humains qui rendent cette vision intenable. En dehors des êtres humains, il n'y a pas que des cailloux. Le monde n'est pas fait de deux catégories d'objets suffisamment distincts pour que le problème du critère éthique ne se pose pas. Il n'est pas évident qu'un chimpanzé n'est pas sensible, qu'il n'a pas de dignité, ni de libre-arbitre. Et s'il y a un doute pour les chimpanzés, il y en a un pour les chats; et pour les poissons, et pour les poulpes, les fourmis et les méduses, et même peut-être aussi pour les plantes. Le corail est un animal, au demeurant proche de la méduse; mais le corail ne ressemble-t-il pas beaucoup à un caillou? Y aurait-il enfin un doute pour les cailloux? Sans doute que non, mais nous aimerions savoir pourquoi.
La question animale, en mettant simplement le doigt sur l'existence des animaux, et donc d'une continuité au moins apparente entre le monde des êtres humains et celui des cailloux, nous force donc à reconnaître la nécessité d'un critère de patience morale susceptible de s'appliquer à tout objet du monde. Les objets de la physique sont donc, tous, au moins potentiellement, des objets de l'éthique; la question de leur possession de telle ou telle caractéristique pertinente pour l'éthique – et en premier lieu, de la sensibilité – peut, pour chacun d'entre eux, recevoir une réponse positive ou négative, mais n'est jamais dépourvue de sens.
Dès lors, la solution qu'adopte notre société pour «résoudre» la double impossibilité, consistant à séparer chacune dans son propre domaine, ne fonctionne plus. Les deux impossibilités se rencontrent et se heurtent dans un même domaine, celui du non-humain. Nous ne pouvons croire que «se demander jusqu'où, en descendant l'échelle des espèces animales, il y a encore quelque forme de conscience» soit une question dépourvue de sens; nous en aurons besoin pour déterminer si nous avons ou non des obligations morales envers ces objets non humains. Cela sera vrai même si nous adoptons les éthiques les plus hostiles à la prise en compte des animaux non humains; si notre critère est non la sensibilité, mais la possession ou non de la rationalité, par exemple, nous aurons besoin de pouvoir l'appliquer à tout objet du monde, fut-ce pour pouvoir montrer en définitive que seuls les humains sont rationnels.
À partir de là, il ne sert plus à rien non plus de chercher à préserver le domaine de l'humain des atteintes de la physique; nous devons accepter qu'il n'y a qu'un monde, et que nous sommes pleinement de ce monde; et que la sensibilité, ou toute autre caractéristique que nous jugeons pertinente pour l'éthique, est de ce monde, et relève, à ce titre, de la physique. Nous devons reconnaître pour l'éthique et la physique le même domaine d'étude, le même monde. L'éthique se soucie du plus humble caillou, au moins en ce sens que ses critères doivent pouvoir nous dire si et pourquoi nous devons, ou non, nous en soucier.
Les critères de l'éthique doivent s'appliquer à tous les objets du monde physique, et c'est seulement par des moyens physiques que nous pourrons déterminer si ces objets satisfont, ou non, à ces critères. Si notre critère est la sensibilité, nous ne pourrons déterminer si un objet est sensible qu'en l'observant. Et nous savons que tout ce que nous observerons – ses mouvements, les sons qu'il émettra peut-être, et ainsi de suite – sont des faits physiques, et sont reliés, par les lois de la physique, à des processus se déroulant dans l'objet. Si nous pensons que ces faits observés sont des indications de la sensibilité de l'objet, alors même qu'ils sont causés par des processus physiques se déroulant dans l'objet, la sensibilité doit être elle-même un phénomène physique. Le même raisonnement vaut pour tout autre critère éthique que l'on pourrait vouloir se donner.
Une physique en crise
Dès lors, nous n'avons pas de solution au problème de la double impossibilité, sauf celle de réviser nos conceptions de la physique. Dans les prochaines sections, après avoir mis en lumière la première impossibilité, à savoir le caractère incontournable du point de vue subjectif et l'impossibilité de ne pas croire certaines choses, je me tournerai vers les raisons de la seconde impossibilité, celle qu'il y a à intégrer la sensibilité et d'autres objets subjectifs dans la vision dominante de la physique. On pourra penser: d'accord, mais la physique moderne semble presque inattaquable, trop pour que l'on puisse la subvertir à partir du seul problème éthique du statut moral des animaux. Je reconnais la force de la physique moderne. Je sais cependant aussi qu'elle est en crise profonde, qu'elle a perdu ses bases. La solidité qu'on lui accorde généralement correspond pour une part à ses succès pratiques, au formidable pouvoir que nous en tirons pour maîtriser la matière; mais aussi, à sa capacité supposée à fournir une image cohérente et compréhensible du monde. Or, de fait, elle a perdu cette capacité depuis l'avènement de la mécanique quantique dans les années 1920. L'image précédente, aujourd'hui caduque, d'une physique expliquant la réalité est pourtant restée par défaut la vision dominante, l'idéal de la physique, tant auprès du grand public que dans l'esprit de la grande majorité des scientifiques, même de ceux à qui la mécanique quantique est familière. Elle l'est restée précisément parce que la mécanique quantique ne nous donne plus aucune conception crédible de rechange.
Je crois cependant cet idéal classique, celui d'un déterminisme calculable, de type «boules de billard», lui-même incohérent, indéfendable en dernier ressort; parce qu'il est incompatible avec la sensibilité, mais aussi parce que si on porte sa logique jusqu'à son terme, il s'auto-dissout en une pure abstraction mathématique dépourvue de substance. Par conséquent, nous ne devons pas espérer sortir de la crise de la physique moderne, quantique, par un retour au paradigme précédent, comme l'ont rêvé des physiciens tels qu'Einstein aux premiers temps de la mécanique quantique. Nous devons plutôt, je crois, nous appuyer sur les «bizarreries» de la mécanique quantique, et sur les contraintes qui résultent de la réalité de la sensibilité, pour tenter d'imaginer ce que pourrait être une autre conception du monde.
J'exposerai plus loin (section 5) les éléments de la structure de cette physique préquantique qui seront utiles à mon propos. Je ne tenterai par contre pas de brosser un tableau de la mécanique quantique, et ne ferai que me référer quand cela sera utile à quelques-unes de ses caractéristiques. On trouvera dans le commerce de bons ouvrages d'introduction à la mécanique quantique qui permettent de se faire une idée de la structure étrange de cette théorie dont l'interprétation la plus orthodoxe nie l'existence d'une réalité objective10.
Le cri de la carotte
Si la prise au sérieux de la question animale et de la question de la sensibilité a des implications profondes concernant nos conceptions physiques, je pense qu'inversement une réflexion sur la physique, et au moins la conscience de l'insuffisance et de l'incohérence de nos conceptions traditionnelles de la réalité physique, peut permettre de dépasser des débats stériles et d'apporter un début de réponse valable à certaines objections qui nous sont faites. Un exemple est le fameux «cri de la carotte». Au-delà de la mauvaise foi certaine qui la motive, cette objection exprime de façon presque explicite le malaise dû à l'impossibilité d'intégrer la sensibilité dans notre vision du monde physique. On ne nous répond pas «et le cri de la carotte?» si nous plaidons en faveur des Tchétchènes; ceux-ci sont humains, et on ne pose donc pas la question du critère physique justifiant leur prise en compte éthique; elle est automatique. Mais si nous nous préoccupons pour des non-humains, même aussi proches de nous que les cochons ou les vaches, cela montre implicitement que nous ne croyons pas en cette partition; nos critères doivent alors nécessairement être physiques. On nous renvoie donc un phénomène physique – le crissement de la carotte que l'on râpe – en nous sommant de le distinguer d'un cri, de l'expression d'une souffrance, puisque nous ne réservons pas cette notion de souffrance au seul monde humain, mais acceptons qu'elle fasse partie du monde physique, du monde des cailloux.
Aujourd'hui, nous pouvons répondre, bien sûr, que la carotte n'a pas de système nerveux, et ainsi de suite. Mais il faut admettre que dans le fond nous ne savons pas montrer en quoi ces critères ne sont pas arbitraires. Qu'est-ce que le tissu nerveux a de particulier qui en ferait le siège unique d'une souffrance potentielle? Ce qui nous manque, c'est une théorie de la souffrance; et une vision globale du monde physique qui rende cette théorie possible. Dès lors, nous pourrons, effectivement, dire de l'extérieur si tel ou tel phénomène constaté – cri ou crissement, par exemple – correspond ou non à une souffrance, sans plus avoir besoin d'être «dans la peau» de la carotte que nous n'avons besoin d'être dans la peau d'un électron pour déterminer dans quel état il se trouve.
3. L'argumentation par l'impossibilité de ne pas croire
On peut distinguer trois sortes de «raisons de croire» en la vérité d'une assertion:
A. Les raisons démonstratives (informations rendant probable l'assertion; croire que demain il pleuvra, parce que la météo le dit, et que la météo se trompe rarement).
B. Les raisons éthiques (en particulier, pour l'utilitariste, il est juste de croire une chose dès lors que cette croyance augmentera le bonheur total dans le monde).
C. Les raisons causales (toute cause dont la croyance est l'effet; la plupart des gens croient aux dogmes de telle ou telle religion parce que leurs parents et proches y ont cru).
Il peut sembler bizarre de voir une finalité comme raison de croire une chose (raisons de type B.). Pourtant, pour les actes en général, c'est bien généralement une finalité que l'on invoque comme raison de l'accomplir.
On peut penser que le raisonnement idéal en faveur d'une thèse doit être du type A, dont le modèle est peut-être le raisonnement mathématique, où on ne fait pas appel à l'utilité pour le lecteur de croire à la vérité du résultat (ce qui en ferait une argumentation éthique) et où on ne cherche pas non plus par exemple à l'hypnotiser pour qu'il croie en cette vérité («argumentation» du troisième type). Que le lecteur soit content ou non que le carré de l'hypoténuse soit égal à la somme des carrés des deux autres côtés du triangle rectangle, on lui montre qu'il en est ainsi.
Seules les raisons de croire de type A peuvent constituer une réponse valable à une question «pourquoi crois-tu que...?». Une réponse de type «j'y crois parce que cela vaut mieux pour moi (ou pour autrui)» ne peut remplacer une raison de type A11. De même si je réponds que c'est à cause de mon éducation, ou parce que mes neurones sont configurés de telle ou telle manière. De telles réponses peuvent être vraies par ailleurs, mais ne sont pas des réponses à la question posée.
Mon intention est de montrer que les assertions éthiques (prescriptives) correspondent à une vérité objective, et de là montrer en particulier le caractère de réalité objective de la sensibilité et de la liberté. Je serais heureux si je pouvais baser ces développements uniquement sur des raisons de type A. Mais je ne le peux pas.
Vais-je alors me tourner vers une argumentation de type B, et vous donner simplement envie de croire que j'ai moi-même plaisir à croire? Ou encore, trouver moyen de vous persuader par des astuces de rhétorique de la justesse de mes idées? En fait, non. Je crois justifié de faire appel dans le cas présent à une autre forme d'argumentation encore. Elle ne consiste pas à donner une raison de croire, mais à mettre en évidence le fait que nous croyons déjà, et ne pouvons pas ne pas croire12. Dès lors, prendre acte de ce fait n'est qu'une question de cohérence.
On peut trouver faible une telle argumentation, puisqu'elle ne constitue pas une démonstration. Ma réponse est pour une part ad hominem, sans être pour autant, je pense, dépourvue de force. Elle consiste à noter que c'est cette même forme d'argumentation qui fonde en dernier ressort tout ce que nous croyons, à commencer par notre conviction de l'existence d'une réalité.
Ce fait est même universellement reconnu; je vais y revenir dans un instant. Ce qui est remarquable, c'est qu'on n'en fait généralement que peu de cas, considérant l'impossibilité de fonder notre croyance en un monde réel sur un pur raisonnement comme une sorte de curiosité philosophique qui n'enlèverait rien au sérieux de cette conviction; alors que l'impossibilité correspondante dans le domaine éthique – l'impossibilité de fonder la vérité des propositions éthiques sur un pur raisonnement – passe pour la preuve irréfutable du caractère relatif ou conventionnel de celles-ci, ou, pour les personnes religieuses, de la nécessité de les fonder sur la foi en un dieu.
Je pense au contraire que le caractère de vérité des assertions éthiques (prescriptives) est autant fondé que celui des assertions dites «descriptives», portant par exemple sur des réalités matérielles13; les unes comme les autres étant fondées sur la même impossibilité de ne pas croire certaines choses que pourtant nous ne pouvons démontrer. Si l'on estime mon argumentation faible, ce ne peut être plus faible que notre croyance en l'existence du monde; ce qui n'est pas rien.
Avant que l'on ne juge de la faiblesse de cet argument, je voudrais encore que l'on en saisisse bien le sens. L'impossibilité de ne pas croire qui le fonde n'est pas une simple difficulté; elle ne se réfère pas par exemple à la pénibilité psychologique qui accompagnerait une non-croyance. Il s'agit d'une impossibilité constitutive de notre façon d'être au monde. Que l'on se figure cela: que du fait de notre présence même dans le monde, de notre situation d'êtres sensibles, il soit impossible que nous ne croyions pas une chose. Il est alors vain de prétendre ne pas y croire. Toute théorie que nous bâtirions et qui contredirait la croyance en question serait impossible à prendre pour vraie sans croire à la fois une chose et son contraire; c'est-à-dire, serait impossible à prendre sérieusement pour vraie, dès lors que nous prenons conscience de ses implications concernant notre croyance obligée. Cela ne nous interdit sans doute pas de spéculer, en imaginant faux ce que nous ne pouvons pas croire faux; nous pouvons éventuellement tirer des conclusions intéressantes de telles spéculations, mais ne pouvons croire réel le monde ainsi construit.
J'en viens maintenant à la substance de l'argument; mon premier pas sera de mettre en lumière en l'impossibilité qu'il y a pour nous de ne pas croire au caractère de vérité réelle des assertions éthiques (prescriptives).
4. L'éthique
L'impossibilité de ne croire en rien
Nous savons souvent clairement si nous croyons ou non une chose. Je crois que nous sommes en ce moment samedi, et je sais que je le crois. Les choses sont pourtant parfois moins simples. Un bon exemple est la question de la foi dans le christianisme, centrale dans cette religion – la condition nécessaire et suffisante pour être «sauvé» étant de croire en Jésus (en son existence, en son caractère divin, en sa résurrection, etc.). D'où ce dilemme lancinant pour tout chrétien: «Est-ce que je crois vraiment?» La simple affirmation – la «profession de foi» – ne suffit évidemment pas. Le récit de Jésus marchant sur l'eau, et de Pierre coulant parce qu'il n'avait pas cru suffisamment fort pouvoir faire de même14, illustre bien le fait qu'on ne sait pas toujours soi-même si l'on croit ou non une chose ou jusqu'à quel point on la croit; car Pierre s'élance, croyant croire, mais ne croyant en fait pas assez; il coule, et Jésus, avec une certaine perversité, lui lance: «Homme de peu de foi, pourquoi as-tu douté?».
Dans cette histoire, c'est le fait de couler ou non qui, de façon surnaturelle, représente le test de la croyance. Un test plus banal est celui-ci: si nous croyons une chose, cela se traduira dans les décisions que nous prendrons.
Croyons-nous en l'existence d'un monde physique? Je ne parle pas de la validité précise de telle ou telle théorie physique, mais dans un sens minimal. Par exemple, est-ce que je crois, moi, à l'existence du clavier devant moi? Il me semble que la réponse est oui; le fait que je tape sur ses touches, dans le but d'écrire ce texte, s'explique par le fait que je crois que cette action va modifier quelque chose dans le monde. Je ne sais peut-être pas en fait très bien définir ce qu'est le monde, ce qu'est la matière, et quel sens cela peut avoir qu'elle soit modifiée; sauf sur un point: je sais quel sens cela a pour les êtres sensibles. Si je tape sur le clavier, je pourrai lire demain ce que j'ai écrit; et d'autres peut-être le liront. Je crois en l'existence du monde au moins en tant que support à une chaîne causale telle que selon la manière dont j'agis, des êtres sensibles – moi-même, pour le moins – en seront affectés.
Le fait que je tape sur ces touches témoigne donc de ma croyance en l'existence du monde, au moins en ce sens minimal du mot «existence».
Cela, dira-t-on, est banal. Cela signifie cependant que beaucoup de monde croit en l'existence du monde! Tous les êtres sensibles, en fait, à mon avis; mais pour le moment, on admettra que cela paraît plausible au moins pour tous les êtres humains adultes typiques – non en état de coma, par exemple. Ils mangent, ils croient donc en l'existence de ce qu'ils voient dans leur assiette, ou au moins au fait que de quelque manière les mouvements qu'ils font leur apporteront ou leur enlèveront quelque sensation, de plaisir ou de faim.
Conclusion banale, certes, mais qui contredit une tradition qui remonte au moins jusqu'au sceptique grec Pyrrhon (IVe-IIIe siècle avant J.C.), lequel disait douter de l'existence même de ce monde. Selon Diogène, Pyrrhon croyait si peu au témoignage de ses sens qu'il n'évitait de tomber des falaises que grâce à l'intervention de ses amis**. C'est là un cas bien rare; pourtant, si ce récit témoigne sans doute d'une non-croyance chez ce philosophe en l'existence de la falaise (si l'on écarte les soupçons sur ce qu'il aurait fait en l'absence de ses amis), il n'implique pas la non-croyance dans le monde en général, au contraire; car pourquoi donc Pyrrhon mettait-il un pied devant l'autre, si ce n'était pour avancer, ou au moins pour soulager l'envie de bouger – laquelle impliquait déjà une croyance en un effet, jamais tout à fait immédiat, de ses actes?
De fait, Descartes, reprenant cette même question de la fondation ultime de nos croyances en l'existence du monde, commença par «douter» de tout; mais ce doute n'était chez lui que provisoire, heuristique, et n'impliquait pas de conséquences pratiques15:
(...) avant de commencer à rebâtir le logis où on demeure (...) il faut aussi s'être pourvu de quelque autre où l'on puisse être logé commodément pendant le temps qu'on y travaillera; [donc] afin que je ne demeurasse point irrésolu en mes actions pendant que la raison m'obligerait de l'être en mes jugements et que je n'en laissasse pas de vivre dès lors le plus heureusement que je pourrais, je me formai une morale par provision, qui ne consistait qu'en trois ou quatre maximes <(...).
Ces «trois ou quatre maximes» pratiques sont empreintes d'un solide bon sens et visent, comme le dit Descartes, à son bonheur, c'est-à-dire à une sensation. Descartes fait découler l'action de la croyance (le «jugement»), puisqu'il craint de demeurer «irrésolu en [ses] actions pendant que la raison [l]'obligerait à l'être en [ses] jugements»; pourtant, il affirme pouvoir suppléer à cette absence de croyance par une morale «par provision» (provisoire). Il semble clair pourtant que cette morale suppose forcément elle-même une croyance. La première, par exemple, «était d'obéir aux lois et coutumes de mon pays»; il croyait donc en l'existence de ce pays. Descartes n'a ainsi jamais réellement cessé de croire en la réalité du monde; il n'a jamais été irrésolu en ses jugements sur ce point, son doute, provisoire, ne portant que sur leurs fondements.
Par ces exemples je veux suggérer que l'existence d'un scepticisme philosophique ou autre quant à l'existence du monde n'implique pas celle d'un doute réel sur ce sujet. Il ne s'agit pas pour moi de dire que ces personnes sont de mauvaise foi. Descartes lui-même ne prétendait pas vraiment avoir cru à l'inexistence du monde. D'autres ont sans doute cru croire, mais, je pense, n'ont eux non plus jamais cru16.
Mais mon propos n'est pas simplement de constater que tel ou tel n'a pas réellement douté de tout, ni même d'affirmer que personne n'a jamais nourri réellement un tel doute; il est de montrer qu'un tel doute est impossible, du fait de notre situation – situation qui est celle de tout être délibérant, et donc, je crois, de tout être sensible.
Notre situation est que nous devons à chaque instant décider. Ce n'est pas que nous avons intérêt à décider; c'est qu'il est impossible que nous ne décidions pas.
Supposons que nous ne croyions en rien. Nous ne croyons alors pas que notre action aura tel ou tel effet. Pourquoi alors nous fatiguer à agir? Nous pourrions aussi bien rester à ne rien faire. Mais pourquoi ne rien faire? Pour moins nous fatiguer? Si nous ne croyons en rien, nous ne croyons pas non plus qu'agir nous fatiguera, ni que ne pas agir nous fatiguera moins.
Nous ne pouvons non plus décider sans raisons. Lorsque nous sommes irrésolus, nous cherchons une raison pour décider d'une manière ou d'une autre; nous ne pouvons décider qu'avec une telle raison. Pourtant, tant que nous demeurons irrésolus, nous avons au moins décidé une chose – à savoir, de ne rien décider d'autre. Nous pourrions courir dans tous les sens, ou prendre une quelconque autre décision; si nous ne le faisons pas, c'est bien que nous avons une raison de ne pas le faire, si ce n'est que, par exemple, pour ne pas nous fatiguer inutilement. Descartes, pour ne pas «demeurer irrésolu», adopte une morale, c'est-à-dire un système de raisons pour décider d'une façon ou d'une autre; mais il ne choisit pas n'importe quelle morale. En même temps qu'il expose ses «trois ou quatre maximes», il les justifie; par des raisons pratiques, «raisonnables» comme on dit, auxquelles de toute évidence il croit, malgré le «doute» que lui impose la raison.
Descartes croit donc en des raisons pour décider, au sens «factuel»; c'est-à-dire qu'il croit en l'existence d'un certain pays, celui où il réside, en l'existence de ses lois et coutumes, etc. Mais il croit en ces raisons aussi au sens prescriptif: il croit que ce sont là des raisons pour décider de se comporter de telle ou telle manière. Il croit en l'existence de raisons prescriptives.
En somme:
— il nous est à chaque instant impossible de ne pas prendre de décisions;
— nous ne pouvons prendre de décisions sans croire en des raisons pour les prendre (raisons prescriptives);
— il nous est donc impossible de ne pas croire en des raisons pour prendre des décisions (raisons prescriptives).
Points de vue intérieur et extérieur
Je crois bon d'insister ici quelque peu sur la position à partir de laquelle on aboutit à cette conclusion. Il s'agit de ce que j'appelle le «point de vue intérieur ». On pourrait imaginer décrire les mêmes événements – une personne en train de délibérer, puis de décider et d'agir – d'un point de vue extérieur, comme un système physique traversant une suite d'états en fonction de certaines lois. Peut-être identifierons-nous alors certains de ces états comme étant des croyances en ceci ou cela; et constaterons-nous que le système est toujours dans un état de croyance en quelque chose, et que cet état est déterminant pour l'évolution ultérieure du système (détermine son action future). Sans doute chercherons-nous aussi à expliquer cet état de croyance, par le jeu des lois du mouvement des atomes, ou, à un autre niveau, par les mécanismes darwiniens d'évolution. Ce point de vue extérieur est valable dans son principe, puisque nous sommes dans le monde, et sommes donc des systèmes physiques; ces descriptions et explications sont forcément possibles. Cependant, pour légitime qu'il soit, le point de vue extérieur ne peut abolir le point de vue intérieur. Le point de vue extérieur constate et explique notre croyance; mais le constat et l'explication de notre croyance ne sont pas notre croyance, et n'abolissent pas, de par leur simple existence, notre croyance.
Il arrive cependant que la manière dont nous constatons et expliquons une de nos croyances constitue une raison de ne plus y croire; par exemple lorsque nous expliquons une illusion d'optique. Il se peut alors que nous abandonnions cette croyance. Mais il se peut aussi que ce ne soit pas le cas, et que nous n'abandonnions pas cette croyance, parce que nous n'avons pas été convaincu par l'explication, ou parce qu'elle ne nous paraît pas réellement contraire à la croyance, ou pour toute autre raison; en tout état de cause, nous ne devons pas nous persuader nous-même que nous ne croyons pas, tant qu'en réalité nous croyons. Et telle sera toujours la situation concernant certaines choses, si, comme je l'affirme, il nous est impossible de ne pas y croire, du fait de notre condition d'êtres délibérants.
Un reproche souvent fait à l'encontre des descriptions et explications scientifiques des phénomènes subjectifs est celui de «réductionnisme». Je pense que ce reproche est, dans le fond, juste; non que nous ne devions pas décrire et expliquer ces phénomènes en des termes scientifiques, ni qu'il faille ajouter à cela, comme on cherche souvent à le faire, une couche holistique de «phénomènes émergents» basés sur le principe contestable selon lequel le tout serait plus que les parties. Je crois plutôt que ces descriptions et explications sont elles-mêmes faites dans les termes d'une physique en réalité incompatible avec les phénomènes subjectifs, et que les accepter reviendrait à accepter que ce point de vue extérieur puisse abolir le point de vue intérieur. Or cette abolition, comme je l'ai dit, n'est pas possible. Une physique qui a des implications auxquelles nous ne pouvons pas croire est elle-même une physique à laquelle nous ne pouvons pas croire.
La réalité de la valeur de vérité des assertions prescriptives
En première ligne parmi les choses auxquelles nous ne pouvons pas ne pas croire se trouve l'existence de raisons pour prendre des décisions, c'est-à-dire l'existence de la bonne réponse à la question «Que faire?». Les réponses (bonnes ou mauvaises) à cette question sont des assertions non pas descriptives, au sens classique du terme, mais prescriptives. Elles sont de la forme «Faire telle chose!». Elles ne s'identifient pas à une simple prédiction, du type «Je ferai telle chose».
On pourra trouver mystérieuse cette nouvelle catégorie d'assertions. Quelle est leur valeur de vérité? En quel sens la proposition «Faire telle chose!» peut-elle être vraie? Tout d'abord, un telle proposition a bien une négative: «Ne pas faire telle chose!». D'autre part, la croyance ne constitue pas en elle-même la vérité de ces propositions; nous sommes susceptibles de nous tromper. Après avoir pensé «Faire telle chose!», nous pouvons nous raviser: «Non, au contraire, faire telle autre chose!». Nous pouvons aussi nous raviser après coup: «Je n'aurais pas dû faire telle chose.» Si la croyance en l'assertion constituait sa vérité, nous ne pourrions pas changer d'avis, c'est-à-dire estimer avoir eu tort; et l'acte de délibération lui-même n'aurait aucun sens – toute conclusion à laquelle nous aboutirions serait de ce fait même juste. Ce serait comme décider de chercher dans un pré le brin d'herbe que l'on y aura trouvé.
Si la valeur de vérité des assertions prescriptives n'est pas constituée par le fait que nous croyions en leur vérité, c'est qu'elle existe indépendamment de notre opinion sur le sujet. Chercher la bonne réponse à «Que faire?», c'est nécessairement supposer qu'une certaine réponse est la bonne, qu'on la trouve ou non. Cela n'aurait pas de sens de la rechercher si nous ne croyions pas cela; mais il est impossible que nous ne la cherchions pas, et il est donc impossible que nous ne croyions pas qu'une certaine réponse est bonne, indépendamment de notre perception de ce fait. C'est en ce sens que nous ne pouvons pas ne pas croire en la réalité de la valeur de vérité des assertions prescriptives.
Fins et moyens
Il ne faudrait pas croire que la délibération se résumerait à une recherche purement factuelle, du genre «Sachant que j'ai telle fin, quel est le meilleur moyen pour y parvenir?». Si tel était le cas, ce que j'appelle «assertion prescriptive» se réduirait à une assertion descriptive, au sens habituel: «Sachant que j'ai telle fin, faire telle chose est le meilleur moyen pour y parvenir». Mais nous choisissons aussi nos fins. Même un être tout à fait «égoïste» choisit de ne prendre en compte que ses propres intérêts, à l'exclusion en particulier de ceux des autres. Cela implique au minimum qu'il croie au caractère factuel de l'éventuelle satisfaction future de ses intérêts, c'est-à-dire, s'il conçoit ses intérêts en termes d'obtention de plaisir et de non-souffrance, qu'il croie en la réalité de son plaisir et de sa souffrance17. Il ne peut croire que constituent une fin pour lui des choses qui, en réalité, n'existent pas. Mais il devra aussi croire que ce plaisir et cette souffrance futurs peuvent résulter de ses propres actes; il devra donc croire en l'existence d'un monde physique, au moins en ce sens minimal. Enfin, la satisfaction de ses propres intérêts représentera au moins dans la plupart des cas non une fin, mais plusieurs finalités au moins partiellement contradictoires; il devra choisir entre des plaisirs qualitativement différents, entre des plaisirs proches dans le temps et d'autres lointains, décider si tel plaisir vaut telle souffrance nécessaire pour l'obtenir...
On peut imaginer aussi que les «intérêts» d'un individu soient définis par lui-même en d'autres termes que le plaisir et la souffrance; deux exemples sont l'idée (résultant d'une mauvaise interprétation du darwinisme) selon laquelle nos «vrais» intérêts seraient la propagation de nos gènes; et celle d'un certain individualisme romantique pour qui il s'agirait par exemple de «nous réaliser nous-mêmes»18. Si certaines personnes prennent vraiment au sérieux de telles finalités, cela ne fait que confirmer la pluralité de nos fins possibles, et donc le fait que celles-ci, comme nos moyens, résultent d'un choix.
Je crois qu'en réalité cette séparation entre choix des fins et choix des moyens est artificielle. Dans nos délibérations réelles les deux sont intimement mêlés. Sans doute la tentation de postuler une telle séparation et de chercher à éliminer le choix des fins en faisant de celles-ci des constantes vient-elle de notre difficulté à concevoir sur quelles bases ce choix pourrait se faire, dès lors qu'il est libre. Je reviendrai sur le problème du libre-arbitre. Je voudrais seulement suggérer ici que le choix des moyens, dès lors que les fins seraient fixées, n'est pas forcément moins problématique quant à son mécanisme. Les solutions trouvées pour atteindre une fin donnée sont souvent «innovantes», et les hypothèses avancées par Penrose suggèrent que notre cerveau permet des modes de résolution des problèmes qui ne pourraient être simulés par un algorithme, et ne sont donc pas déterministes au sens du déterminisme calculable.
Un sens «pour moi»?
Nous ne pouvons nous abstenir de décider, et ne pouvons décider sans nous demander «Que faire?»; et nous ne pouvons nous poser cette question, comme n'importe quelle question, que si nous lui accordons un sens.
Nous ne pouvons pas dire, «oui, j'accorde un sens à cette question, mais c'est parce que ne peux faire autrement; mais je ne crois pas qu'elle en possède un réellement». Si nous ne croyons pas qu'elle a réellement un sens, nous ne croyons pas qu'elle en ait un du tout.
Nous ne pouvons pas non plus dire, «oui, elle a un sens, mais seulement pour moi». Ce procédé de relativisation est souvent utilisé aussi concernant les assertions «descriptives» au sens classique. Il me semble bon d'en examiner la signification.
«Pour moi» peut vouloir dire «c'est là ce que je crois»; alors «x a un sens pour moi» signifie «je crois que x a un sens (mais d'autres, peut-être, ne le croient pas)». L'assertion selon laquelle x a un sens n'est alors pas elle-même relative, mais absolue. Je peux dire, «pour moi la terre est plate»; la platitude de la terre reste une question absolue: elle est vraie ou fausse indépendamment de moi. Affirmer que les assertions prescriptives ont un sens pour un certain individu, c'est alors affirmer que cet individu croit qu'elles ont un sens absolu; et c'est bien là ce que j'ai voulu montrer: nous croyons tous que les assertions prescriptives ont un sens.
Dans d'autres cas, le «pour moi» dénote un autre type de relation entre l'énoncé et un certain individu. Une pomme peut avoir un goût sucré pour Anne, et acide pour Valérie; son «goût objectif» n'existe alors pas. Cela ne signifie cependant pas que le goût qu'il a objectivement pour Anne n'existe pas, comme celui qu'il a pour Valérie! Dans le cas qui nous occupe, on pourrait donc dire que l'avoir-un-sens de x est une vérité objective, mais en relation avec moi. Cette relation pourrait être le simple fait qu'effectivement, c'est moi qui crois que x a un sens; nous retrouvons alors la première interprétation du «pour moi». La relation pourrait aussi être le fait que l'assertion prescriptive x est elle-même clairement en relation avec l'entité «moi», du moins si on admet l'existence d'une telle «identité personnelle»19: elle prescrit ce que je dois faire. Il s'agit d'une vérité me concernant, en ce sens; mais d'une vérité à laquelle je crois, tout comme je crois (ou non) à la platitude de la Terre.
Il est remarquable que cette relativisation – ce «vrai pour moi» – fonctionne comme si «moi» était une entité en quelque sorte extérieure au monde, et pouvait à ce titre en quelque sorte emmener dans sa retraite la vérité elle-même dont il s'agit. Dès lors que nous faisons partie du monde, notre point de vue lui-même sur le monde en fait partie. Si nous croyons que les assertions prescriptives ont un sens «pour nous», nous croyons qu'elles ont un sens tout court.
L'éthique comme théorie de la réponse vraie à «Que faire?»
J'ai jusqu'à présent parlé d'assertions prescriptives; je crois que nous pouvons aussi les appeler assertions éthiques. Plus exactement, je pense qu'une assertion prescriptive – l'assertion «Faire telle chose!» – est vraie si la chose qu'elle commande de faire est celle que nous commande de faire l'éthique; et par conséquent que la délibération – le fait de se poser la question «Que faire?» – est la recherche de l'action éthiquement juste.
Je ne le dis pas dans un sens normatif; c'est-à-dire, je n'affirme pas que toute délibération devrait être la recherche de l'action éthiquement juste. Je dis que de fait elle l'est. Je pense que l'éthique doit se définir ainsi: comme théorie de la réponse juste (vraie) à la question «Que faire?».
On me dira que je suis libre de définir mes mots comme je l'entends, mais que mon «éthique» n'est tout simplement pas l'éthique au sens courant du terme. Je ne crois pas une telle objection justifiée. Plus exactement, je crois que la définition que je donne de l'éthique découle de l'usage habituel du terme, dès lors que l'on cesse de faire une exception arbitraire concernant les décisions qui ne concernent que soi-même, et que l'on admet le caractère de vérité absolue des assertions prescriptives.
On oppose généralement comportement égoïste et comportement éthique. L'éthique aurait justement pour fonction de nous amener à penser aux autres, à respecter leurs droits et leurs intérêts, plutôt que de ne penser qu'à nous-mêmes. Certaines conceptions éthiques sont explicitement restrictives concernant leur domaine d'application; les théories contractualistes, par exemple, nous enjoignent, pour l'essentiel, de respecter les termes de notre «contrat» avec autrui, mais en dehors de cela, nous laissent «libres» de faire «selon notre bon vouloir»20. Une théorie éthique au moins, cependant, régit en principe la totalité de nos choix, en mettant sur un pied d'égalité ceux qui concernent nous-mêmes et ceux qui concernent autrui. En effet, pour l'utilitarisme hédoniste, nous devons agir pour maximiser le bonheur net dans le monde; dès lors, un acte augmentant notre propre bonheur sans affecter celui d'autrui est éthiquement obligatoire, au même titre que peut l'être un acte augmentant le bonheur d'autrui.
Ce fait est rarement perçu, peut-être tout simplement parce qu'il y a peu besoin de commander aux gens de rechercher leur propre bonheur. Un tel commandement reste pourtant de nature éthique, même si nous y adhérons en général sans le secours d'une théorie éthique construite. Il en est de même pour beaucoup de propositions de la physique; nous n'avons pas besoin de la mécanique des fluides pour boire un verre d'eau. La physique n'en serait pas moins artificiellement mutilée si nous retirions de son domaine de compétence ce qui se passe quand nous buvons un verre d'eau; tout comme c'est une mutilation artificielle de l'éthique que d'en retirer les prescriptions «évidentes» comme celles qui nous commandent de tenir compte de nos propres intérêts.
Parmi les théories éthiques fréquemment mentionnées, il y en a une autre au moins qui nous donne des obligations dans les choix ne concernant que nous-mêmes. Il s'agit de ce qu'on appelle «l'éthique égoïste», dont le commandement unique est: maximise ton propre bonheur. Le fait qu'elle soit fréquemment mentionnée en tant qu'éthique, même comme «cas d'école»21, montre que l'usage n'exclut pas, au moins en théorie, du champ de l'éthique les décisions ne concernant que nous-mêmes. Cette éthique égoïste, tout comme l'utilitarisme hédoniste, gouverne en principe la totalité de nos choix.
Cependant, la raison fondamentale qui me fait dire que l'éthique doit se définir comme la théorie générale de la réponse vraie à «Que faire?» est le fait que toute délibération est fondamentalement altruiste. Même si je suis en train de ne penser qu'à «moi-même», je pense nécessairement à un «moi-même» futur. Mes actes ne peuvent déterminer le plaisir ou la souffrance que j'éprouve au moment où je les choisis; ils détermineront forcément mon plaisir ou ma souffrance futurs. Nous sommes habitués à trouver évidente la préoccupation que nous avons pour nous-mêmes. Le problème fondamental de justification de l'éthique nous semble être «pourquoi devrais-je, rationnellement, me préoccuper d'autrui?»; et c'est une question que beaucoup estiment dépourvue de réponse. Il est bien rare par contre que nous nous demandions «pourquoi devrais-je, rationnellement, me préoccuper du bonheur ou du malheur que j'éprouverai dans cinq minutes?». Nous pouvons pourtant tout aussi bien déclarer que ce bonheur ou malheur futur nous est totalement indifférent! Il est rare que l'on soit totalement indifférent à ce que l'on éprouvera dans cinq minutes, tout comme il est rare que l'on soit totalement indifférent au sort des personnes proches; par contre, il est fréquent que l'on soit assez indifférent à ce que l'on éprouvera dans trente ans. Si ce n'était pas le cas, la consommation de tabac s'en ressentirait.
L'idée selon laquelle il y aurait une différence radicale entre le souci pour ses propres intérêts – forcément futurs – et celui pour les intérêts d'autrui me semble donc une construction dogmatique et artificielle, peu justifiée tant au niveau théorique que pratique. C'est en ce sens que je crois que toute délibération est altruiste; les intérêts qu'elle prend en compte sont toujours ceux d'un «autre», que cet autre soit un autre individu, ou un soi-même futur.
«J'ai du mal à y croire»
Il reste une objection à cette conception de l'éthique: nos décisions ne sont pas, de fait, toujours conformes à l'éthique, même à l'éthique à laquelle nous-mêmes adhérons. Il est parfaitement possible de dire «je reconnais que je devrais faire telle chose, mais je ne parviens pas à m'y résoudre»22.
Je crois cependant que cette objection tombe si nous envisageons les assertions prescriptives comme possédant une valeur de vérité réelle, indépendante de la connaissance que nous en avons. Ce n'est pas notre adhésion verbale à une prescription qui en fait la valeur de vérité; ce n'est pas non plus le fait que nous croyions y adhérer.
Il peut être utile de faire le parallèle avec les assertions descriptives, au sens classique. Quand un parachutiste débutant ne parvient pas à sauter dans le vide, n'est-ce pas parce qu'il n'est pas tout à fait convaincu que cet acte est sans danger? Il pourra bien protester qu'il sait que cela est sans danger; et il pourra repasser cent fois dans sa tête les données qui devraient le rassurer. Mais il faut bien croire que «quelque chose en lui» continue à croire au danger. Il me semble que cela implique pour le moins que nous ne sommes pas tout à fait des «individus», des atomes. Si je crois que la conscience n'est pas une illusion (à quels yeux le serait-elle?), il me semble que son unité, par contre, est illusoire, au moins en partie. Par conséquent, le fait qu'une partie de notre conscience soit convaincue d'un fait n'interdit que d'autres parties soient convaincues du contraire.
Nous savons souvent sans savoir. «J'ai du mal à y croire» dit-on souvent au sujet de la mort d'un proche. Il se peut bien en effet que nous agissions parfois comme si ce proche était encore là; que nous mettions encore le couvert pour lui, «par distraction» – ou plutôt, parce qu'une partie de nous ne croit toujours pas en sa mort.
Pour revenir aux assertions prescriptives: nous pouvons bien savoir que ce que nous allons faire n'est pas ce que nous devrions faire; parce que, par exemple, cela va faire souffrir autrui, plus que cela ne va nous faire plaisir. Mais nous le savons sans le savoir entièrement; tout comme nous savons, par exemple, que le plaisir de cette cigarette nous fera peut-être beaucoup souffrir plus tard, tout en ayant du mal à y croire. C'est donc bien parce qu'une partie de nous ne croit pas vraiment à ce que, pourtant, nous croyons croire que nous agissons en contradiction avec ce que nous croyons croire; et ceci est vrai, que ce que nous croyons croire soit de l'ordre du descriptif (au sens classique), ou du prescriptif.
Il y a quelques mois je suis monté au sommet d'une des tours de la Basilique de Fourvière à Lyon. Cette tour, ouverte aux visites, est gravie par des centaines de personnes tous les jours, depuis des lustres; je savais qu'elle n'allait pas s'écrouler simplement parce que je mettais un pied de travers! Tout me démontrait que la probabilité en était infime. Pourtant, j'eus le vertige en grimpant les marches; un vertige rempli de craintes de l'écroulement de l'édifice. Je posais le pied doucement, de peur de faire des chocs. Je suis arrivé au sommet, mais les dents serrées. Cette peur était sans doute irrationnelle, elle n'en était pas moins réelle; elle correspondait bien à une croyance réelle en moi, celle de courir un danger.
Je ne vois pas de difficultés à considérer le problème de la non-observance de nos propres croyances éthiques sous le même angle. Nous n'y croyons, tout simplement, qu'en partie.
Description et prescription
Ma thèse est que nous croyons aux prescriptions comme nous croyons aux descriptions; nous croyons ce qu'elles nous disent vrai (ou faux). J'utilise encore à leur sujet d'expressions comme «vérité objective», «réalité». Une phrase célèbre – dont je ne retrouve pas l'origine, et que je cite de mémoire – disait en substance qu'on ne trouve nulle part dans l'univers quelque chose qui ressemblerait à une prescription; et que les prescriptions, par conséquent, n'existent pas en soi. Les devoirs moraux, le bien et le mal, ne seraient que le fruit de nos préférences personnelles «subjectives», d'origine culturelle ou autre. Il n'y aurait pas de vraie éthique.
J'admets ne pas pouvoir définir clairement moi non plus en quel sens les prescriptions éthiques sont des objets réels. Je crois cependant que l'idée généralement reçue sans discussion selon laquelle les objets «matériels», eux, existent, est largement aussi problématique. Le verbe «exister» semble transparent, mais la transparence rejoint l'opacité dans le fait de ne laisser voir aucun contenu. De fait, dans la physique moderne, quantique, la question de l'existence même d'une réalité objective est devenue d'une grande opacité; la position «standard» (dite «de Copenhague») est qu'elle serait elle-même dépourvue de sens. La physique ne serait qu'un ensemble de «recettes» permettant de prédire les observations futures à partir des observations passées. Tout le reste ne serait que «spéculation gratuite»23. Paradoxalement, selon cette interprétation, l'utilité (humaine), objet subjectif, voire prescriptif, reste seule en lice – la réalité physique a disparu, animaux non humains compris.
La mécanique classique, préquantique, que j'appelle «laplacienne», semble, elle, donner à la réalité physique une plus grande consistance. C'est elle, comme je l'ai dit, qui est restée une sorte d'idéal de la physique, y compris auprès d'esprits scientifiques, avides d'une croyance en une réalité dure et froide. On perçoit donc peu à quel point, en fait, la logique même de la physique laplacienne conduit elle aussi à une dissolution de la notion de réalité. Je vais consacrer la section suivante à une description sommaire de cette conception laplacienne du monde, et à mettre en relief quelques-unes de ses faiblesses.
En tout état de cause, je voudrais que l'on suspende quelque peu les certitudes habituelles selon lesquelles pour être «réelle», une «chose» doit être faite en matière et se trouver «quelque part dans l'univers». Nous ne savons pas bien ce qu'est être réel pour un caillou. Nous ne savons pas non plus très bien en quel sens les vérités mathématiques existent. Je ne saurais non plus dire précisément en quel sens les assertions prescriptives existent. Je sais seulement que l'on ne peut ôter toute existence ni aux cailloux, ni aux vérités mathématiques, ni aux vérités éthiques. Je crois que ces choses existent dans le monde, et donc y existent objectivement, y sont réelles. Je ne ferai pas de distinctions nettes entre ces notions, parce que je ne crois pas à celles que l'on fait habituellement.
En particulier, je pense que si une assertion prescriptive, de la forme «Faire telle chose!», est vraie, c'est qu'elle décrit une réalité. On oppose classiquement le descriptif et le prescriptif; je pense au contraire que toute assertion est descriptive. C'est pourquoi aussi je parle d'assertions descriptives «au sens classique» pour celles que l'on considère habituellement comme telles (sur la masse des cailloux, par exemple).
Les animaux en tant qu'agents moraux
Dans les théories morales antispécistes, il est courant de distinguer la notion d'agent moral de celle de patient moral. Les humains sont généralement à la fois agents moraux, c'est-à-dire qu'ils peuvent (et doivent) agir de manière éthique, et patients moraux, c'est-à-dire qu'on doit tenir compte d'eux (de leurs intérêts, droits, dignité...) lors d'une décision éthique. En revanche, les animaux non humains ne sont généralement considérés que comme patients moraux: on doit se soucier d'eux, autant que des humains, mais ils n'ont pas de devoirs, parce qu'ils ne sont pas capables de raisonner à un niveau éthique, tout comme les jeunes enfants humains par exemple.
Si l'on accepte par contre, comme je le propose, que toute délibération est par définition une recherche éthique, et qu'il n'y a pas de différence de nature entre la prise en compte par l'individu délibérant de ses propres intérêts (futurs) et des intérêts d'autres êtres, on conçoit que tout animal, dès lors qu'il délibère, est un agent moral, dans le même sens où un humain peut l'être.
Cela ne signifie pas qu'il n'y ait pas à faire de distinctions dans le niveau de complexité et d'abstraction que peut atteindre un individu dans son raisonnement éthique. Il en va pour l'éthique comme pour la physique. Les animaux qui délibèrent sont aussi nécessairement des physiciens; ils prévoient des conséquences à leurs actes. Seuls quelques-uns parmi eux, à savoir certains humains, peuvent bâtir des théories physiques et/ou éthiques complexes et abstraites; bien plus souvent, l'horizon éthique et physique est plus restreint; on s'en tient aux choses que l'on voit, à l'avenir immédiat, à ses propres intérêts prochains et à ceux de sa famille ou de son groupe. Cette éthique et cette physique limitées n'en sont pas moins une éthique et une physique.
Nos cris de peur et de douleur disent: «Ce n'est pas bien!» Les cris du cochon que l'on égorge disent la même chose: que ce n'est pas bien. C'est ce que dit aussi l'antispéciste; il dit que ce n'est pas bien, pour les mêmes raisons que le dit le cochon. Cette même proposition, dans des bouches différentes, a le même sens et la même nature; c'est une proposition éthique.
Si l'on en croit les paroles que l'écrivain végétarien J.M. Coetzee met dans la bouche d'un de ses personnages24, c'est l'éthique d'une poule qui, en partie, fit abolir la peine de mort en France:
Pour ce qui est de l'idée selon laquelle les animaux seraient trop muets et stupides pour parler en leur propre nom, pensons à la séquence d'événements suivante. Quand Albert Camus était enfant en Algérie, il advint que sa grand-mère lui demanda d'aller lui chercher une poule dans les cages de la cour. Il obéit, et vit ensuite sa grand-mère couper la tête de la poule avec un couteau de cuisine et recueillir le sang dans un bol pour éviter de salir par terre.
Le cri d'agonie de la poule s'imprima dans la mémoire de l'enfant et ne cessa de le hanter au point de l'amener à écrire en 1958 une dénonciation passionnée de la guillotine. Ce fut en partie suite à cette polémique que la peine de mort fut plus tard abolie en France. Qui peut donc dire que la poule ne pouvait pas parler?
5. Le modèle laplacien de la réalité
Ce que j'appelle modèle classique, ou laplacien, de la réalité naquit au XVIIe siècle avec Galilée et Newton, en remplacement de la physique d'Aristote dominée par les idées finalistes, animistes, de nature et de finalité des corps. Le modèle laplacien constitua le socle du rationalisme scientifique et domina la vision scientifique du monde jusqu'au début du XXe siècle. La théorie de la relativité d'Einstein (1905, 1915) se place encore dans ce cadre, qui ne fut subverti que dans les années 1920, par la mécanique quantique – laquelle le rendait intenable, sans pour autant apporter de vision alternative de la réalité physique.
Je pense que l'on se rendra compte, en lisant la courte analyse que je vais faire ici de ce modèle, que c'est bien celui que nous tendons «spontanément» à voir comme le modèle de description scientifique. Lorsque nous tenons absolument, par exemple, à rejeter l'idée de libre-arbitre parce qu'il «faut bien» que nos choix soient déterminés par quelque chose, cette exigence n'est évidente ni dans le cadre aristotélicien, ni dans celui de la mécanique quantique, laquelle implique que certains événements se produisent effectivement sans raison. Je ne crois pas non plus le modèle, ou plutôt non-modèle, que nous donne la mécanique quantique satisfaisant pour rendre compte du libre-arbitre; mais je voudrais au moins que l'on accepte de relativiser quelque peu les postulats du modèle laplacien. Je montrerai d'ailleurs en quoi ce modèle ne satisfait pas lui-même à ses propres exigences qui voudraient que tout arrive pour une raison.
J'appelle ce modèle «laplacien» en référence à cette formulation frappante que le physicien Pierre Simon de Laplace (1749-1827) donna de la notion de déterminisme25:
Une intelligence qui, pour un instant donné, connaîtrait toutes les forces dont la nature est animée et la situation respective des êtres qui la composent, si d'ailleurs elle était assez vaste pour soumettre ces données à l'analyse, embrasserait dans la même formule les mouvements des plus grands corps de l'univers et ceux du plus léger atome: rien ne serait incertain pour elle, et l'avenir, comme le passé, serait présent à ses yeux.
Dans cette vision des choses, la réalité – tout ce qui existe – est constituée d'une collection finie ou infinie d'objets – les «êtres» dont parle Laplace – dont chacun peut être caractérisé par un certain nombre de propriétés éventuellement variables dans le temps; la connaissance à un instant donné de la liste de ces objets et de leurs propriétés constitue une description complète de la réalité en cet instant.
Une image simplifiée que j'utiliserai souvent est celle des boules de billard. Dans un jeu de billard idéalisé, en effet, les boules se meuvent à tout instant suivant une loi parfaitement définie et calculable. Tant qu'elles ne rencontrent pas une paroi ou une autre boule, elles se meuvent en ligne droite à vitesse constante; lors d'une collision, elles rebondissent de manière élastique, suivant une loi simple qui met en jeu leurs caractéristiques intrinsèques (masse, rayon), leur mouvement et leur position. L'évolution de l'ensemble peut être complexe, si un grand nombre de boules sont en jeu, mais reste toujours entièrement prévisible, au moins en théorie, par une «intelligence», comme l'appelle Laplace, qui connaîtrait les lois du mouvement ainsi que la masse et la situation (position, vitesse) de chaque boule. L'image «boules de billard» du monde suppose que le monde entier n'est qu'une vaste collection de telles boules se mouvant dans l'espace à trois dimensions.
Bien entendu, la physique classique n'a jamais sérieusement proposé une vision aussi simpliste des choses. L'image «boules de billard» reste cependant valable, parce que la physique classique se ramène bien, conceptuellement, à une telle image, à quelques nuances près. Dans la physique classique, nous n'avons pas des boules, mais des «points matériels» – «atomes» ou «particules» sans dimensions, mais possédant par exemple une masse et une charge – et des forces attractives et répulsives de forme plus complexe que la simple répulsion par «contact». À ces points matériels s'ajoutèrent par la suite les champs, comme le champ électrique, répartis dans tout l'espace, servant de médiateurs aux forces entre particules, mais évoluant aussi eux-mêmes selon leurs propres lois. Dès lors, la connaissance exhaustive dont parle Laplace implique aussi celle des champs, et donc une infinité de données, puisqu'il faut connaître l'intensité des champs en chaque point de l'espace26. Il n'en reste pas moins que le modèle «boules de billard» possède toutes les caractéristiques que je vais mentionner du modèle laplacien. Si la subjectivité ne peut trouver sa place au sein d'un modèle «boules de billard», elle ne peut la trouver au sein de la physique laplacienne27. Je me permettrai ainsi souvent de parler comme si celle-ci n'était réellement constituée que de boules de billard, parce que c'est là une image simple qui permet d'en faire ressortir les caractéristiques et les problèmes.
Notons que la physique classique n'est jamais parvenue à proposer une théorie à la fois cohérente et plausible de la réalité; il restait toujours des détails qui clochaient dans les coins28. L'image laplacienne n'en subsiste pas moins comme paradigme de toute physique qui se veut objective, qui croit en une réalité indépendante de l'observateur, puisque la mécanique quantique s'avère incapable de fournir un tel modèle.
La complétude du modèle laplacien
La complétude signifie que tout ce que l'on peut dire du monde est réputé contenu dans la «situation respective des êtres qui [le] composent»; c'est-à-dire, pour reprendre l'image des boules de billard, dans la position et la vitesse de chacune d'entre elles.
En particulier, le mouvement de nos mains, nos pensées, nos sentiments, tout cela ne serait constitué que de l'entrechoquement «mécanique» de ces boules selon les lois du mouvement. Dire que nous percevons le monde, c'est seulement dire que certaines de ces boules, celles du monde extérieur à notre corps, heurtent d'une certaine manière les boules de notre corps, qui, en raison de leur disposition initiale, vont de proche en proche provoquer certains mouvements et dispositions de certains autres ensembles de boules dans notre cerveau ou ailleurs, mouvements et dispositions qui devront, d'une manière ou d'une autre, constituer la perception. Nos sentiments et émotions seront de la même manière constitués par des dispositions et mouvements de boules quelque part en nous. Lorsque nous agissons en fonction de nos perceptions et sentiments, ce sera parce que ces dispositions et mouvements auront à leur tour, toujours suivant les mêmes lois «mécaniques» du mouvement, provoqué certains mouvements dans d'autres ensembles de boules encore, que nous appelons nos mains, qui écriront nos observations sur une feuille de papier.
Du fait de cette complétude, les boules ne possèdent elles-mêmes aucune «intériorité». L'expression «boules de billard» est trompeuse sur ce point. La physique des boules de billard réelles en mouvement sur une table de billard décrit quelques unes de leurs caractéristiques, comme leur position et leur vitesse de déplacement, mais ces paramètres sont relatifs à des objets qui existent par ailleurs et qui possèdent bien d'autres caractéristiques: couleur, rugosité, composition chimique, solidité... Par contre, dans le modèle laplacien type «boules de billard», les boules n'ont aucune couleur ni rugosité; elles ne sont pas faites de «quelque chose». Tout ce que l'on peut dire d'elles se résume en une petite collection de nombres, à savoir leur masse, leur rayon, leur position et leur vitesse. Le «rayon» lui-même ne correspond pas à la limite entre un intérieur plein et un extérieur vide, mais à un simple paramètre déterminant si et quand aura lieu une «collision» avec une autre boule. Cette «collision» ne sera qu'un changement dans le mouvement du «centre»; mais de quoi est-ce donc le centre? De rien; ce n'est qu'un point mobile dans l'espace déterminant des «collisions», c'est-à-dire des événements touchant d'autres «boules», qui elles-mêmes ne sont que des points du même genre. Pourtant, l'espace est rempli de points; qu'est-ce que ceux-ci ont de particulier? Rien, à part que leur position est celle décrite par cette collection de nombres...
Si jamais il y avait autre chose à dire de cette réalité, si les «boules» possédaient une réalité au-delà de ces quelques nombres, celle-ci nous serait absolument inconnaissable; car la connaître ne serait rien d'autre que des positions et mouvements particuliers de certaines boules dans notre cerveau, et, en vertu du déterminisme du modèle, ces positions et mouvements sont entièrement déterminés à partir de ceux de toutes les autres boules, et ne peuvent donc en rien dépendre de cette autre réalité.
Comme déjà indiqué, l'image réelle que proposait la physique laplacienne, fondée sur les particules et les champs, est bien plus complexe que le modèle «boules de billard». L'absence d'intériorité reste cependant entière; le monde n'a pas de «substance» et reste totalement descriptible par une collection de nombres, qui semblent ne rien décrire d'autre qu'eux-mêmes. Dès lors, on voit mal en quoi il serait autre chose qu'une collection de nombres. Il est paradoxal de voir que la conception laplacienne, souvent ressentie comme le summum du «matérialisme», paraît en définitive dissoudre le monde en une abstraction idéaliste.
Un déterminisme réversible
Le modèle laplacien est déterministe, dans un sens défini par la citation ci-dessus: le monde est régi par un ensemble de lois tel que si je connais l'état du monde à un instant donné (l'ensemble des nombres qui le décrit), je peux en principe déduire (calculer) son état à tout instant futur. Le mot «déterminisme» renvoie cependant à autre chose encore, à une relation de cause à effet: que l'état du monde futur est entièrement causé par son état présent. Cette interprétation courante est déjà suggérée par l'origine du mot: l'avenir serait déterminé, c'est-à-dire causé, par le présent, puisqu'un état présent donné ne peut engendrer qu'un seul état possible futur. Il semble ainsi naturel d'identifier le déterminisme physique, laplacien, à un principe de causalité totale («tout ce qui arrive est déterminé par ce qui est arrivé»); paradoxalement, comme je le montrerai, la notion même de causalité est dépourvue de substance dans le déterminisme laplacien.
Il est significatif que Laplace ait fait jouer dans sa citation un même rôle au passé et à l'avenir: «et l'avenir, comme le passé, serait présent à ses yeux». De fait, tous les modèles classiques de la physique sont réversibles par rapport au temps. Cela signifie, en termes imagés, que si je filme n'importe quel événement, et passe ensuite la séquence à l'envers, la séquence inversée que je vois reste conforme aux mêmes lois d'évolution. Cette propriété est vérifiée dans le modèle «boules de billard»: tant le mouvement rectiligne uniforme que les changements de mouvement lors des chocs sont réversibles.
C'est là encore une propriété de toutes les théories physiques réelles, y compris, à quelques nuances près, des théories quantiques29.
Le déterminisme laplacien implique que si je connais l'état du monde à l'instant présent, il ne peut donner qu'un seul état à un instant futur; mais du fait de sa symétrie passé/avenir, il implique aussi que l'état présent ne peut résulter que d'un seul état possible à un instant passé. Est-ce à dire que le présent cause le passé? Le présent «détermine» autant le passé que le futur, si on entend par détermination le fait que pour un présent donné, il ne peut y avoir qu'un seul passé, tout comme il ne peut y avoir qu'un seul futur. Or, le déterminisme laplacien ne dit rien de plus. La notion de causalité, toujours dissymétrique – le passé cause l'avenir, mais non l'inverse – ne peut donc être légitimée sur cette seule base.
Ce paradoxe illustre le fait que la réversibilité laplacienne est contraire au sens commun: nous n'avons pas du tout le sentiment que le passé et l'avenir soient symétriques. Le temps nous semble avoir une «flèche» bien définie, ne pouvoir «aller» que dans un sens; et les causes sont bien d'un côté – que nous nommons passé – et leurs effets de l'autre – que nous nommons avenir. Il semble pourtant impossible de faire découler une telle flèche d'équations d'évolution tout à fait symétriques; le problème de la «flèche du temps» représente depuis le XIXe siècle une des difficultés majeures de la physique.
Je reviendrai plus loin sur la notion de causalité parce qu'elle est liée à celle de loi – elle-même problématique dans le cadre laplacien – et à celle de libre-arbitre, qui constitue à mon sens un des ingrédients incontournables du subjectif.
L'hypothèse épiphénoméniste
L'épiphénoménisme est la théorie selon laquelle la sensibilité (subjectivité, conscience) ne serait qu'un épiphénomène du monde physique; c'est-à-dire, en deux mots, qu'elle peut regarder mais pas toucher. Il s'agit moins d'une thèse qui serait réellement défendue que d'une conclusion désagréable à laquelle semblent mener bon nombre de tentatives de rendre compte de la sensibilité dans le cadre d'une conception laplacienne de la réalité.
J'ai dit plus haut qu'en vertu de la complétude du paradigme laplacien, nos sensations, sentiments et émotions y sont nécessairement constitués par des «dispositions et mouvements de boules», ou, dans les termes d'un modèle plus réaliste, par la disposition et le mouvement des particules et l'état des champs à l'intérieur de notre cerveau.
Intuitivement, beaucoup de personnes, dont moi-même, trouvent difficile de croire que la sensibilité puisse n'être «que» cela. Pour le moins, on ne voit pas très bien en quoi des mouvements de particules et autres processus «mécaniques» peuvent constituer une sensation; les sensations et phénomènes subjectifs semblent impliquer autre chose. Je reviendrai sur des justifications plus argumentées qu'on peut apporter à ce sentiment. Je veux juste noter ici que si l'on cherche à faire de la sensibilité «autre chose», tout en restant dans le cadre du modèle laplacien, on aboutit nécessairement à une position épiphénoméniste.
Formellement, l'idée selon laquelle la sensibilité serait autre chose que le simple mouvement des boules de billard est d'emblée en contradiction avec l'hypothèse de complétude du modèle laplacien, qui implique précisément qu'il n'y ait rien de plus dans le monde que ce qui est dans ce modèle. Nous pouvons cependant imaginer un modèle «laplacien-plus», formé d'un monde, disons, «physique», celui des boules de billard, qui se comporterait de manière purement laplacienne, plus cet «autre chose», la sensibilité, qui serait le siège des sensations. Lorsque le feu brûle notre main, par exemple, cela mettrait en mouvement une certaine succession de mouvements dans les boules formant notre main, lesquels de proche en proche influeraient sur les boules dans notre cerveau, qui à leur tour amèneraient les boules formant notre bouche à pousser un cri; parallèlement à cela, l'état des boules dans notre cerveau ne constituerait pas la douleur, mais la provoquerait dans cette «autre chose» spectatrice siège de la sensibilité.
Une telle conception, qui semble à même de résoudre notre difficulté à concevoir la sensibilité au sein du monde laplacien tout en conservant à celui-ci un rôle de théorie du «monde physique» (auquel viendrait cependant s'ajouter un monde psychique), implique nécessairement l'épiphénoménisme. En effet, on y suppose que la sensibilité est affectée par ce qui se passe dans le monde laplacien; elle est informée de la douleur, ou plutôt des dispositions des boules de billard qui correspondent à la douleur. Il ne paraît pas impossible de lui attribuer une telle position passive; il est par contre impossible de lui faire jouer un rôle actif sans rompre, justement, le déterminisme du monde laplacien. Les boules de billard évoluent en fonction de leur état et de celui des autres boules de billard; ce serait une dérogation à ces lois que de permettre à la conscience, à notre volonté, d'agir sur leur évolution. Et on ne peut admettre une telle dérogation sans faire entrer de plain-pied la conscience dans le monde physique, lequel ne serait plus ni laplacien ni «laplacien-plus30».
Voilà donc ce qui mène à envisager la position épiphénoméniste, selon laquelle la conscience serait affectée par le monde physique, mais ne pourrait en retour agir sur celui-ci. Il me semble par ailleurs qu'un certain nombre de thèses qui ont cours parmi les philosophes qui réfléchissent à ce domaine impliquent l'épiphénoménisme. Je pense en particulier à la position B dans la classification de Penrose dont je parlerai en section 8, position qui est celle du philosophe John Searle. Il est cependant rare que les partisans de ces thèses adhèrent explicitement à la position épiphénoméniste, car il est difficile d'y adhérer consciemment.
Elle signifie en effet que rien dans notre comportement ne résulte du fait que nous soyons conscients. Cela implique que lorsque nous crions de douleur, par exemple, nous ne crions pas réellement de douleur; la douleur, la volonté que cela cesse et toutes les autres perceptions sont ressenties par la subjectivité spectatrice, mais ne jouent aucun rôle causal dans nos cris, qui ne sont dus qu'à la mécanique insensible des «boules de billard». Les souvenirs, même, que nous avons de nos propres émotions ne sont alors pas des souvenirs d'émotions, mais l'effet subjectif d'un état «purement physique» présent se «souvenant» d'un certain état «purement physique» passé, lequel, par ailleurs, produisait (peut-être) à ce moment-là un certain état subjectif.
Si l'épiphénoménisme était vrai, nous ne pourrions pas le savoir; ou plutôt, nous ne pourrions pas le dire, ou ne le dirions que «par hasard». L'épiphénoménisme correspond à une tentative d'expliquer la conscience, le fait que nous ressentons les choses; mais il nie justement que nos actions, et donc en particulier nos discours au sujet de l'épiphénoménisme, puissent résulter d'une quelconque manière de ces sensations! L'épiphénoménisme met la subjectivité sur une voie de garage à sens unique.
Plus généralement, si l'épiphénoménisme était vrai, nous ne pourrions rien savoir de la subjectivité; hormis peut-être notre propre subjectivité instantanée. Nous ne pourrions prévoir les conséquences de nos actes sur notre subjectivité future, puisque nous ne pouvons nous baser sur aucune véritable expérience de leurs conséquences passées. Il n'y aurait aucun sens à délibérer, et ceci doublement: parce que nous ne pourrions baser nos choix sur rien, et parce que nos choix ne pourraient agir sur rien.
Si on admet ma thèse selon laquelle nous sommes des êtres délibérants, et ne pouvons croire que la délibération n'a pas de sens, on admettra que nous ne pouvons croire à la position épiphénoméniste.
Il faut noter cependant que la définition que j'ai donnée de l'épiphénoménisme dépend de la notion de causalité, qui est elle-même problématique dans le cadre laplacien. Je ne veux pas développer ce point ici, mais seulement mettre en évidence le fait que l'épiphénoménisme, solution tentante, est une solution fausse.
Test de Turing
Le nom du mathématicien britannique Alan Turing est plutôt méconnu du grand public; il est pourtant pour beaucoup dans un des thèmes centraux de la science-fiction et de cette attente quasi messianique que nous avons eue de «l'an 2000»: le mythe du robot pensant, voire désirant ou même pathétique comme Hal dans 2001 Odyssée de l'espace. Cette thématique présente l'ordinateur comme un équivalent artificiel du cerveau humain, et suggère – plus souvent qu'elle n'affirme – que ces êtres, dès lors qu'ils se montrent capables de se conduire (à peu près) comme des humains, sont peut-être réellement sensibles et pensants.
Je parle de mythe; car au moins pour l'instant cela reste un mythe. Nous avons bien aujourd'hui des machines que l'on appelle «robots», mais qui ont peu à voir avec ces Hal et autres R2D2. Rien, certainement, qui puisse donner le sentiment de vraiment penser, et encore moins d'éprouver des émotions.
C'est dans un article écrit en 1950 que Turing posa la question: «Les machines peuvent-elles penser31?». S'interrogeant sur la définition des termes «machine» et «penser», il remplace immédiatement la question initiale par une autre, qui lui serait «étroitement liée». Celle-ci est: «Est-il possible qu'une machine réussisse au “jeu de l'imitation”?». Ce test, que Turing décrit alors, est resté sous le nom de «test de Turing».
Il s'agit de faire «converser» à distance la machine avec un humain, appelé «l'interrogateur», qui ne sait pas s'il a affaire à une machine ou à un être humain. La «conversation» se passe par télétype, c'est-à-dire par l'équivalent 1950 de nos claviers et écrans. La machine peut penser, dit en substance Turing, si elle est capable de tromper l'interrogateur dans une conversation de plusieurs minutes en se faisant passer pour un humain.
Turing propose de définir le fait de penser par la capacité à réussir ce test. C'est du moins ce que suggère sa manière d'introduire le test, ainsi que plusieurs autres réflexions contenues dans l'article. D'autres passages pourtant, ainsi que le bon sens, donnent le sentiment contraire; j'y reviendrai. Par ailleurs, c'est sans ambiguïté qu'il définit ce qu'il entend par «machine» en spécifiant qu'il s'agit d'ordinateurs, c'est-à-dire de dispositifs dont le comportement est entièrement déterminé par un programme, ou algorithme.
Son opinion était que «d'ici environ cinquante ans il sera possible de programmer des ordinateurs (...) de manière à ce que leur habileté au jeu de l'imitation amène l'interrogateur moyen à n'avoir pas plus de 70% de chances d'identifier correctement l'être humain après cinq minutes d'interrogation32.» L'an 2000 est maintenant passé et cette prédiction s'est révélée fausse. Malgré la puissance technique des ordinateurs, qui dépasse nettement celle que prévoyait Turing, et malgré plus de cinquante ans d'efforts de la part d'un grand nombre d'équipes de recherche en «intelligence artificielle» dans le monde, aucun programme sur aucun ordinateur n'est aujourd'hui capable de passer pour un être humain ne serait-ce que 30 secondes.
On peut distinguer trois affirmations dans la thèse de Turing:
(a) Le fait qu'un système pense peut se définir par un tel test, c'est-à-dire par le fait de pouvoir exhiber le même comportement qu'un humain33.
(b) Le fait qu'un système pense peut se déduire de son comportement.
(c) Un ordinateur peut penser, c'est-à-dire se montrer capable du même comportement qu'un être humain.
L'affirmation (b) est une conséquence immédiate de (a): si la pensée se définit par le comportement, elle peut certainement se déduire du comportement. La réciproque n'est cependant pas vraie. Le réalisme – la croyance en l'existence d'un monde réel – implique que les choses existent, d'une manière ou d'une autre, par elles-mêmes, et que nous ayons ou non les moyens de nous assurer de cette existence. Cela reste vrai même si, de fait, nous avons toujours ces moyens. Même si nous pouvons toujours savoir s'il fait jour en regardant dehors, le fait qu'il fasse jour ne se définit pas par l'opération de regarder dehors.
On appelle «opérationnalisme» ce point de vue qui consiste à admettre, au contraire, que les notions scientifiques doivent se définir par des opérations effectuées sur le monde. Ce sera par exemple de définir la température d'un corps par la position du mercure dans un thermomètre construit de telle et telle façon, mis en contact avec le corps d'une certaine manière pendant un certain temps.
L'opérationnalisme repose implicitement sur la séparation du monde en humains et en cailloux. Car qui est ce «nous» censé, en somme, faire exister le monde, si ce n'est l'ensemble des humains? Mais c'est une version particulière de cette séparation, où en définitive les cailloux n'existent pas par eux-mêmes; elle est par conséquent incompatible avec le réalisme, et donc, en particulier, avec la conception laplacienne du monde, qui présuppose que ce monde existe. Pourtant, le credo opérationnaliste fait partie du bagage standard de l'esprit scientifique moderne, cohabitant sans trop de heurts avec le paradigme laplacien. Là encore, en fait, il y a partage des champs d'application; l'opérationnalisme fait surtout surface dans les domaines scientifiques qui paraissent échapper au paradigme laplacien, comme la thermodynamique34, la mécanique quantique et – c'est justement ce qui nous intéresse ici – la psychologie.
C'est suivant le critère opérationnaliste que le «rationaliste» de Schrödinger déclare que la sensibilité (ou la non-sensibilité) d'un animal n'a pas de sens: c'est qu'on n'a pas de critère pour la mettre en évidence. Turing par contre affirme que chez les humains et les ordinateurs, la sensibilité a un sens, mais qui se réduit à la réussite à son test. Plus loin, il répond à l'objection selon laquelle la pensée, les émotions et autres sensations sont des choses réelles en affirmant, en substance, que cette négation de (a) implique celle de (b) et doit donc être rejetée35, parce que conduisant au solipsisme.
D'autres passages semblent pourtant indiquer qu'il ne prend pas réellement son test au sérieux comme définition de la pensée. Il se demande par exemple si, par ailleurs, «les machines n'effectuent pas certaines opérations que l'on devrait décrire comme une forme de pensée très différente de celle qu'accomplit l'homme36», forme de pensée qui ne serait pas prise en considération par son test. Si pourtant il considérait vraiment son test comme une définition de la pensée, on ne pourrait supposer qu'autre chose doive être considéré comme une pensée. Enfin, sa définition conduirait à considérer beaucoup d'humains comme incapables de penser; un jeune enfant, un paralytique, une personne ne parlant aucune langue commune avec l'interrogateur, etc., placés dans la situation de la «machine» dans le test, ne le réussiraient pas mieux que ne le ferait un caillou; pourtant, Turing ne paraît pas vouloir exclure de telles personnes. Il semble bien donc qu'il ait à l'esprit que son test est bien cela, un test, et non une définition; un test implique l'existence a priori de la chose testée, et en même temps son accessibilité (au moins en principe) à l'expérience.
Je crois que les hésitations de Turing traduisent l'impossibilité à prendre vraiment au sérieux le point de vue opérationnaliste, ceci tout particulièrement dans le domaine de la psychologie; car si nous acceptons (a) et définissons la sensibilité par une opération conduite par un observateur, lequel, pour observer, doit lui-même percevoir, c'est-à-dire être sensible, nous obtenons une définition circulaire. Pourtant, si nous rejetons (b), dit Turing, nous n'avons pas de moyen de savoir si un être est sensible; la sensibilité ne peut alors être constatée que par la personne elle-même. C'est pour cela qu'il parle de solipsisme.
Je pense que nous devons effectivement accepter, pour l'essentiel, (b), mais rejeter (a); c'est-à-dire que nous devons admettre que la sensibilité existe en soi, et qu'en même temps son existence ne peut être toujours inaccessible à l'expérience conduite de l'extérieur. Il me semble que nous pouvons aboutir à cette conclusion à partir du raisonnement exposé dans la section 4: s'il était par principe impossible de déterminer «de l'extérieur» qu'un être est ou non sensible, l'éthique serait impossible, tout comme la physique serait impossible s'il était dans tous les cas impossible de déterminer «de l'extérieur» l'état d'un système physique. Nous nous retrouverions dans la situation postulée par l'épiphénoménisme: une sensibilité réelle mais sans action sur le monde.
Je n'ai cependant pas encore analysé le lien entre éthique et sensibilité. J'y reviendrai dans la section 8, pour établir ces conclusions de manière un peu plus rigoureuse.
Notons qu'accepter (b) en ce sens ne signifie pas que dans chaque cas il est effectivement possible constater cette sensibilité. Il fut impossible à Galilée de cartographier la face cachée de la lune; il se peut aussi que nous ne parvenions pas à déterminer, aujourd'hui, si les mouches sont sensibles ou non. La face cachée de la lune et la sensibilité ou non-sensibilité des mouches n'en sont pas moins des réalités, qui ne se définissent pas par la possibilité que «nous» aurions d'en prendre connaissance. Ce double aspect d'accessibilité et d'inaccessibilité potentiels me semble essentiel.
Pourquoi Turing semble-t-il croire qu'accepter (b) implique d'accepter (a)? Je crois que c'est parce qu'il accepte (c), c'est-à-dire en substance qu'il est possible de simuler par un ordinateur – donc par l'exécution d'un algorithme – tout comportement d'être sensible. Dès lors, il est impossible de distinguer de l'extérieur un tel ordinateur d'un être sensible. Si nous acceptons (b), nous devons alors conclure que cet ordinateur est, réellement, sensible. Mais par ailleurs, rien dans les entrailles de l'ordinateur ne paraît correspondre à quelque chose comme une sensibilité; nous n'y trouvons que des transistors et des fils, et, à un autre niveau d'analyse, des algorithmes déterminant le comportement. Surtout, aucune théorie n'existe qui nous permette de reconnaître la sensibilité lorsque d'aventure nous la rencontrons; pire, dans le cadre laplacien implicitement admis, nous ne voyons pas à quoi pourrait ressembler une telle théorie – je pense qu'en effet, dans ce cadre, une telle théorie est impossible.
Si nous sommes incapables de trouver la sensibilité dans l'ordinateur, mais devons par ailleurs admettre qu'il est sensible (si on ne peut le distinguer par son comportement d'un être sensible), il ne nous reste plus qu'à le considérer comme sensible, et ceci en vertu de son seul comportement; et donc, faute de mieux, à définir la sensibilité de manière opératoire, par ce comportement.
Si tel est bien le raisonnement sous-jacent de Turing, il est rendu nécessaire par:
– son acceptation de (c);
– l'impossibilité de fonder une théorie réaliste de la sensibilité dans le cadre laplacien.
L'acceptation de (c), en particulier, est une conséquence directe du caractère calculable du déterminisme laplacien. C'est ce point précis qui fonde les thèses de Penrose, qui conclut que la physique réelle du monde ne peut pas être calculable, c'est-à-dire que nous devons rejeter (c). Je suis d'accord avec Penrose sur ce sujet; je pense que nous devons rejeter (c), et dès lors accepter (b) comme test de la sensibilité, en considérant celle-ci comme réelle, plutôt que définie par ce test comme le postule (a).
Nous avons vu que (c) n'a pas été validée dans les délais prévus par Turing; mais cela n'implique pas en soi la fausseté de cette proposition. Ce sont d'autres raisons, que je développerai dans la section 7, qui me font penser qu'il n'est pas possible de simuler le comportement d'un être sensible par un algorithme, et que par conséquent le monde ne peut être calculable. Avant cela, il sera utile de préciser cette notion de calculabilité, et de la distinguer, en suivant Penrose37, du simple déterminisme.
La calculabilité
Le déterminisme implique que si l'état du monde est fixé à un instant donné, son état à un instant futur est déterminé. Le déterminisme calculable implique en plus que cet état futur peut être calculé. On peut croire qu'il s'agit de la même chose, mais ce n'est pas le cas.
Dans le modèle laplacien, le monde peut être décrit à chaque instant par une collection de nombres. Les lois d'évolution nous permettent de calculer, à partir de ces nombres à l'instant t, leur nouvelle valeur en un instant immédiatement subséquent t + dt. Ce calcul peut se décomposer en opérations d'arithmétique élémentaire (addition, multiplication...), lesquelles peuvent être faites par l'application de simples «recettes», c'est-à-dire de manière automatique; en somme, par un algorithme. À vrai dire, pour plusieurs raisons il est rarement possible d'effectuer ce calcul avec une précision parfaite; par exemple, il faudrait le faire avec une infinité de «chiffres après la virgule». Il est cependant toujours possible de le faire avec une précision aussi grande que l'on voudra, du moins en théorie38.
La notion d'algorithme a été formalisée de manière rigoureuse par le même Alan Turing, comme étant n'importe quelle opération dont est capable ce qu'on appelle aujourd'hui une «machine de Turing». Je vais en noter les grandes lignes39. La machine de Turing dispose d'un programme, qui représente l'algorithme particulier qu'elle doit exécuter; il s'agit d'une liste finie (mais aussi grande que l'on voudra) d'instructions. On lui fournit un ensemble de données de départ; dans le cas qui nous intéresse, il s'agira de la description (aussi précise que l'on voudra) du monde à un certain instant t1. En exécutant son programme, elle transforme pas à pas ces données. Au bout d'un certain temps (aussi grand que nécessaire) elle aboutit à une «instruction d'arrêt». Les données qu'elle laisse alors sont le résultat de son exécution, qui représenteront, dans le cas qui nous intéresse, l'état du monde à un autre instant t2 (avec une précision aussi grande que l'on voudra).
Notons que l'algorithme est unique, indépendant des données. Avec cet algorithme unique, nous pouvons obtenir, à partir de n'importe quel état possible du monde en t1, son état en t2.
Il y a là deux faits que nous pouvons distinguer:
– La nécessité. Si le monde à l'instant t1 est dans un certain état instantané I1, alors en l'instant t2 il est nécessairement dans un certain autre état I2.
– La calculabilité. Si je connais I1, je peux calculer, à l'aide d'un algorithme connu d'avance (indépendant de I1), l'état I2.
Il se trouve que ces deux notions ne sont pas identiques; plus exactement, la première n'entraîne pas forcément la seconde. Dans le cas d'une physique laplacienne, les deux sont vérifiées. Il existe cependant des classes de problèmes mathématiques telles qu'à chaque problème particulier de la classe correspond une réponse précise, «nécessaire»; mais où pourtant aucun algorithme n'existe, ni ne peut exister, qui permette d'obtenir cette réponse «mécaniquement» pour tous les problèmes de la classe.
Penrose donne comme exemple d'une telle classe de problèmes celle du pavage du plan par des «pavés» géométriques, comme les trois de la figure 340. Pour ceux-ci, le problème sera: est-il possible, avec ces trois seuls pavés, reproduits indéfiniment, tournés et/ou retournés à volonté, de paver entièrement le plan (infini), sans recouvrements ni trous? Il se trouve que pour ce jeu-là de pavés, la réponse est positive: il est possible de le faire. La figure 3 montre le début d'un tel pavage. Il n'existe cependant pas de pavage périodique avec ces trois pavés; la démonstration de cette réponse positive n'est donc pas simple, mais elle existe.
Pour d'autres jeux de pavés de ce genre, la réponse sera négative. Ce qu'il importe de noter, c'est que pour chaque jeu de pavés (pour chaque problème de la classe de problèmes, donc) la réponse est parfaitement définie; le pavage est possible, ou il ne l'est pas. Nous retrouvons là la notion de nécessité; on peut dire que la spécification d'un jeu de pavés rend nécessaire, ou détermine, la réponse oui, ou la réponse non.
Il a cependant été démontré que cette réponse n'est pas calculable; c'est-à-dire qu'il n'y a aucun algorithme, aucune recette que l'on peut appliquer mécaniquement, permettant de savoir, pour n'importe quel jeu de pavés, s'il peut ou non paver le plan. Certes, pour tout jeu donné de pavés, il existe un algorithme pour cet ensemble qui donne la bonne réponse; en effet, cette réponse est soit oui, soit non, et par conséquent un des deux algorithmes élémentaires «répondre oui» et «répondre non» suffira! Ce qui n'existe pas, c'est un algorithme unique, commun à tous les ensembles de pavés (à tous les problèmes de la classe de problèmes), capable de donner, pour chacun de ces ensembles, la bonne réponse.
Pour un jeu donné de pavés, comment savoir, donc, s'il pave le plan? La seule réponse possible est: chercher une démonstration (de la réponse positive ou négative). En somme: «Réfléchir!». Cette «recette» n'est pas garantie! Nous ne pouvons savoir d'avance, dans le cas général, ni que nous réussirons, ni que nous échouerons. Aucune recette mécanique ne peut le dire. Et si nous trouvons une démonstration, pour le jeu suivant nous devrons recommencer; chaque démonstration sera une innovation.
Nous voyons sur cet exemple de pavage la distinction entre nécessité (déterminisme) et calculabilité. Penrose, à partir de là, montre comment on peut imaginer un «univers» (non plausible, mais peu importe) soumis à une loi d'évolution déterministe mais non calculable. L'état de l'univers est simplement représenté à chaque instant, non par une collection de nombres comme dans le modèle laplacien, mais par un jeu de pavés. La loi d'évolution est telle que l'état de l'univers à l'instant t + 1 dépend du fait que le jeu de pavés correspondant à l'instant t pave ou non le plan. Une telle loi est déterministe, en ce sens qu'à chaque instant le jeu de pavés qui décrit l'état de l'univers pave ou non le plan, ce qui rend l'état suivant nécessaire. Elle n'est cependant pas calculable, puisque aucun algorithme ne permet de passer «mécaniquement» de l'état en l'instant t à celui en t + 1. Un ordinateur, par exemple, serait incapable de prévoir l'évolution d'un tel monde, aussi déterminée soit-elle.
Le modèle laplacien du monde est déterministe, et calculable. La thèse de Penrose est que l'évolution du monde physique ne peut être calculable. Il semble par contre présupposer qu'elle doit être déterministe, comme dans le monde fictif des jeux de pavés que je viens de décrire; ce sera bien évidemment un monde bien plus complexe, dont on peut supposer qu'il intégrerait l'ensemble des connaissances physiques actuelles comme approximation. Penrose recherche une telle non-calculabilité du côté d'une relation entre la gravitation et le problème de la «réduction du paquet d'ondes» en mécanique quantique; et note par ailleurs l'existence dans certaines cellules nerveuses de structures très particulières suggérant la possibilité de tels phénomènes en leur sein41.
La partie constructive de la réflexion de Penrose est très intéressante, mais ne constitue en rien une théorie achevée. En aucune manière, non plus, ne s'en dégage une caractérisation de la sensibilité en tant que telle, c'est-à-dire du fait que nous ressentons les choses, au lieu qu'elles ne fassent que «se produire» de façon insensible. Dans la section 6, je chercherai à détailler quelques interrogations sur la structure même du monde physique qui me semblent encore résulter de certains faits auxquels nous ne pouvons pas ne pas croire. Dans ce cadre, le déterminisme même non calculable du monde physique ne me semble pas une évidence.
Quoi qu'il en soit, la possibilité même d'une non-calculabilité, possibilité qui, de fait, existe dans le domaine mathématique, me semble très suggestive, déjà par le parallèle avec la situation délibérative dont j'ai parlé dans la section 4. Nous croyons en l'existence d'une réponse juste à la question «Que faire?»; cette réponse est déterminée, «existe», au même sens peut-être qu'existe, pour un jeu donné de pavés, la réponse juste à la question «Pavent-ils le plan?». Comment aboutissons-nous à cette réponse juste? Dans le cas des pavés, il n'y a aucune recette; il faut réfléchir. Je suggère qu'il en va de même pour la situation délibérative. Pour répondre à la question «Que faire?», il faut réfléchir. Dans un cas comme dans l'autre, nous savons que la réponse juste existe, mais nous n'avons en général ni recette pour y parvenir, ni garantie d'y parvenir, ni certitude de ne pas pouvoir y parvenir.
Cette distance entre la connaissance et son objet est peut-être essentielle à l'existence de l'un et de l'autre. Ce qui est frappant dans les modèles de déterminisme calculable, c'est que le résultat peut s'obtenir par un algorithme, c'est-à-dire par un procédé où cette relation, dite d'«intentionnalité», entre la connaissance et son objet est inutile, et, de fait, absente. Les données manipulées par l'algorithme n'ont besoin d'avoir aucune signification pour que le calcul procède, et aboutisse à coup sûr au résultat correct. L'algorithme représente une sorte de «réflexion sans substance». On nous présente souvent les animaux non humains comme mus uniquement par des «pulsions». La pulsion détermine directement le comportement; nul besoin pour l'animal de comprendre quoi que ce soit, de décider quoi que ce soit, donc de désirer quoi que ce soit: la pulsion pourrait être directement branchée sur les muscles! Bien sûr, il peut y avoir conflit de pulsions; la vision d'un point d'eau accompagnée de l'odeur d'un prédateur. Fuir ou aller boire? Selon cette conception, c'est la pulsion la plus forte qui l'emporte. Là encore, nul besoin de réfléchir, un pèse-pulsions cérébral de trois neurones suffit. Nul besoin de comprendre qu'il y a un prédateur, d'anticiper un danger, de ressentir une peur du prédateur, un désir pour l'eau, d'évaluer l'existence de points d'eau alternatifs; nul besoin d'une relation intentionnelle, d'un ressenti, d'une substance...
J'ai conscience du caractère flou de ces propos; quelle est donc cette «substance» dont je parle? Ce «manque de substance» me paraît cependant central dans les difficultés de notre science à rendre compte de la sensibilité. Nos sensations sont des choses qui existent en tant que telles; mais la science semble ne vouloir admettre que des choses vides, qui n'existent qu'en relation avec d'autres choses elles-mêmes vides.
La «substance» dont je parle, c'est peut-être simplement l'existence. Mais comment définir le fait d'exister? Ce qui me semble certain, c'est que si nous prenons au sérieux le modèle laplacien, ce mot paraît bien creux. Pour le voir, une petite formalisation de son cadre conceptuel sera utile.
Le cadre conceptuel du modèle laplacien: monde réel, mondes possibles, mondes imaginables
Le modèle laplacien suppose la possibilité de décrire le monde dans sa totalité par un objet mathématique. Dans l'exemple des boules de billard, il s'agira de l'énumération des trois coordonnées de position et de vitesse de chacune des boules à un instant donné, c'est-à-dire, si n boules existent dans l'univers, d'une suite de 6n nombres réels. Le monde est donc entièrement décrit par cette suite, c'est-à-dire par un élément de l'ensemble noté ℝ6n de toutes les suites de 6n nombres réels. Tout ce qui peut être dit du monde à cet instant est contenu dans cet objet; et la connaissance du monde à cet instant permet sa connaissance à tous les instants passés et futurs, c'est-à-dire celle du monde entier dans toute son histoire.
De façon générale, je distinguerai donc le monde instantané – le monde entier à un instant donné – du monde historique, qui est l'univers entier dans la totalité de son histoire passée et future. Cette notion de monde historique peut nous paraître fictive; nous sommes tentés de nous demander: «Quand existe-t-il?» Pourtant, nous pourrions aussi demander à propos du monde instantané «où existe-t-il?», et l'absence de réponse possible dans ce cas ne rend pas fictive la notion de monde instantané. Faut-il qu'un objet existe en un temps, mais non nécessairement en un lieu? Voici une remarque éclairante de Penrose42:
La conscience, après tout, est l'unique phénomène que nous connaissions qui implique que le temps doive de quelque façon «s'écouler»! Le statut du temps en physique moderne n'est pas essentiellement différent de celui de l'espace, et en réalité le «temps» des descriptions physiques ne «s'écoule» en aucune manière; nous avons simplement un «espace-temps» d'allure statique où sont disposés les événements de notre univers! Pourtant, nos perceptions nous indiquent bien que le temps s'écoule (...).
Ce que dit Penrose de la physique moderne vaut déjà pour le modèle laplacien43. Dans ce cadre, si le monde est une réalité, alors le monde historique est la totalité de la réalité, même si cette notion est contraire à nos intuitions. Si celles-ci, comme je le pense, s'avèrent en définitive justes, c'est le modèle laplacien lui-même que nous devrons rejeter; en attendant, puisque nous examinons ici ce modèle, nous devons accepter comme réel le monde historique.
Puisque nous pouvons décrire le monde instantané par un objet mathématique I appartenant à un certain ensemble I – dans le cas des boules de billard, I est l'ensemble ℝ6n – nous pouvons aussi décrire le monde historique par un objet mathématique M appartenant à l'ensemble M des applications qui à n'importe quelle date t font correspondre un certain monde instantané I = M(t).
Nous avons donc deux ensembles: l'ensemble I de tous les mondes instantanés imaginables, dont fait partie, à tout instant, le monde instantané réel; et l'ensemble M des mondes historiques imaginables, dont fait partie l'unique monde historique réel MR – l'indice «R» servant à indiquer qu'il s'agit du monde historique réel.
On peut donner une représentation graphique de cela, si on imagine l'ensemble I des mondes instantanés imaginables comme pouvant être portés sur une droite; c'est là une simplification extrême, puisque en réalité, même dans le cas simple d'un monde de boules de billard, il faudrait non pas une, mais un grand nombre (6n) de dimensions pour représenter cet ensemble; mais elle nous permet de tracer un graphique à deux dimensions, avec les mondes instantanés en ordonnée, et le temps en abscisse (fig. 4).
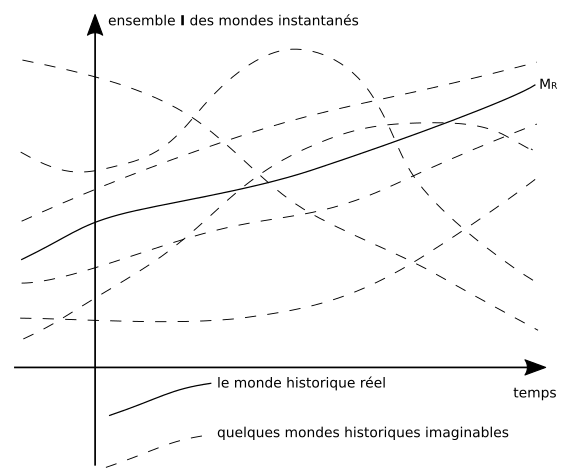
Le monde historique réel MR est alors représenté par une courbe, formée de la succession des mondes instantanés qu'il parcourt au cours du temps. Sur la figure 4, il s'agit de la courbe pleine épaisse. En pointillés sont représentés quelques-uns des innombrables mondes historiques imaginables; n'importe quelle succession arbitraire de mondes instantanés est un monde historique imaginable, une seule de ces successions correspond au monde historique réel.
Quel est dans ce cadre le statut des lois de la physique? Elles nous permettent de déduire l'état réel du monde à n'importe quel instant passé ou futur, dès lors que nous connaissons cet état à l'instant présent. Si nous savons qu'à l'instant t1 le monde est dans l'état I1 nous pouvons en déduire l'état instantané I2 du monde à n'importe quel autre instant t2. Connaissant I1, nous pouvons donc déduire le monde historique réel dans sa totalité; nous sommes dans la position de l'«intelligence» dont parle Laplace, pour qui «l'avenir, comme le passé, serait présent à ses yeux».
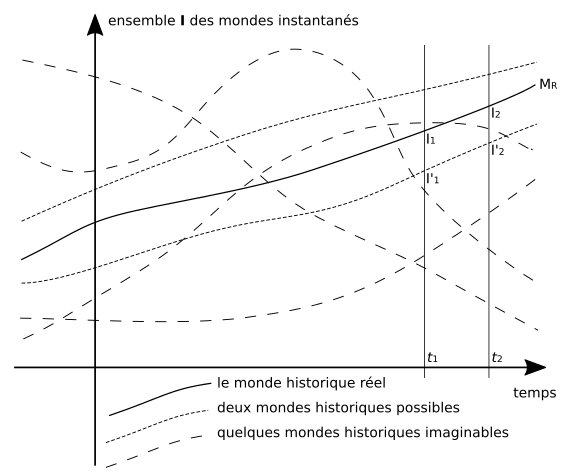
Cependant, ces lois nous disent plus que cela. La loi de la gravitation, par exemple, nous dit non seulement quel sera le comportement des planètes dans le monde réel en orbite autour du soleil réel, mais aussi quel serait leur comportement si elles étaient placées autrement qu'elles ne le sont réellement, ou si le soleil était deux fois plus massif, et ainsi de suite. Les lois de la physique nous permettent donc non seulement de déduire l'état réel I2 du monde à l'instant t2 à partir de son état réel I1 à l'instant t1, mais aussi de déduire l'état instantané I'2qu'aurait le monde en l'instant t2s'il était dans n'importe quel autre état instantané I'1 à l'instant t1 (fig. 5). En somme, elles nous permettent de tracer non seulement la trajectoire correspondant au monde historique réel, mais aussi toute une famille de trajectoires de mondes historiques non réels, mais conformes à ces lois dans leur évolution et que je qualifierai donc de «possibles». J'ai représenté deux de ces mondes historiques possibles (mais non réels) sur la figure 5, par des courbes en pointillés serrés. Ces courbes ne se croisent pas les unes les autres, ce qui traduit le déterminisme des lois (par un point donné ne passe qu'un seul monde historique possible).
Les lois de la physique apparaissent donc comme des règles spécifiant un ensemble des mondes historiques «possibles» parmi un ensemble plus vaste, celui des mondes historiques imaginables. Je peux imaginer que le monde évolue n'importe comment; que je saute par la fenêtre, par exemple, et vole comme Superman. N'importe quelle succession d'états du monde est imaginable. Ce sont les lois de la physique qui me disent que si je saute par la fenêtre, je tomberai plutôt que ne volerai; et donc que le monde où je saute et vole est imaginable, mais non possible. Le monde où je saute et tombe est, lui, possible, mais non réel (car de fait je ne sauterai pas).
Un déterminisme défaillant
L'idée que les choses puissent arriver sans raison parut scandaleuse lorsque fut formulée la mécanique quantique, dans les années 1920; et ce sentiment de scandale perdure et explique une part de la nostalgie éprouvée encore aujourd'hui pour le cadre ancien. Tout à coup, il apparaissait qu'il y avait des questions sans réponse, des choses qui arrivaient «par hasard», comme ça. «Dieu ne joue pas aux dés» aurait protesté Einstein. Dans le cadre laplacien, en effet, tout semblait avoir une cause. L'état du monde aujourd'hui y était entièrement causé par l'état du monde hier, et ainsi de suite, à l'infini. On pouvait toujours trouver un «parce que» à chaque «pourquoi?».
Pourtant, dans le modèle laplacien, il y a un «pourquoi?» – et pas des moindres – qui ne trouve pas de «parce que». Il est bon de le noter, si ce n'est que pour introduire un doute dans notre attachement à un déterminisme absolu et ouvrir notre esprit à d'autres perspectives.
Dans le cadre laplacien, nos «pourquoi?» reçoivent toujours une réponse tant qu'ils ne portent que sur des états instantanés du monde ou d'une partie du monde. Les lois d'évolution déterminent infailliblement les états instantanés du monde réel les uns par rapport aux autres. Mais si nous envisageons cette succession de mondes instantanés comme un tout et fixons donc notre attention sur le monde historique réel MR, rien dans le déterminisme laplacien ne nous dit pourquoi le monde réel doit être celui-là, plutôt que n'importe quel autre monde historique possible. Il nous explique les résultats du loto par la position et la vitesse initiales de chaque balle, mais il n'explique pas pourquoi nous sommes dans ce monde, avec ces positions et vitesses initiales et ces résultats, plutôt que dans un autre, avec d'autres positions et vitesses initiales et d'autres résultats.
Aux personnes qui affirment que Dieu existe puisqu'il faut bien que le monde ait une cause, les athées rationalistes répondent souvent que la cause du monde aujourd'hui, c'est le monde d'hier, et ainsi de suite. L'explication par Dieu est, clairement, une non-explication; mais nous voyons qu'il en est de même de l'explication d'aujourd'hui par hier. Le déterminisme laplacien ne nous apporte, pas plus que la croyance en Dieu, de réponse à ces questions.
6. Causalité, liberté et lois
Sur la base de ce même principe d'impossibilité de ne pas croire certaines choses, j'en viens à deux conséquences qui ont un rapport direct avec la physique, par le fait qu'elles contredisent directement l'image laplacienne du monde.
La première de ces conséquences – la réalité de la relation causale – est habituellement considérée comme allant de soi, et compatible avec la vision laplacienne du monde; elle serait même presque synonyme de la notion de déterminisme qui fonde cette vision. La seconde – la réalité de notre liberté, ou libre-arbitre44 – va elle aussi de soi dans la vie quotidienne, et dans la pratique des tribunaux45, mais elle est paradoxalement perçue comme incompatible avec la vision laplacienne, laquelle impliquerait pourtant que nous en ayons l'illusion.
Je crois pour ma part que la relation causale est bel et bien réelle, mais que, contrairement à l'opinion commune, elle est incompatible avec le déterminisme laplacien. Je crois également que la liberté est réelle, et qu'elle est elle aussi incompatible avec la vision laplacienne.
Enfin, ces deux notions sont liées à celle de loi physique. Il en va pour cette dernière comme pour celle de causalité: elle est, contrairement à ce que l'on croit communément, incompatible avec le déterminisme laplacien. On ne peut pourtant l'abandonner.
Nous devons construire une physique qui admette la réalité de la relation causale, de notre liberté et des lois physiques. Elle ne peut donc être conforme au déterminisme laplacien.
Causalité et déterminisme
La causalité implique une certaine relation, dite de «cause à effet», entre deux événements. Celle-ci n'est pas une simple juxtaposition. Élodie a jeté un caillou par la fenêtre (événement A) tout en prononçant le mot «potiron» (événement B). Le caillou est tombé sur la chaussée (événement C). Nous dirons que A a été la cause de C; mais ne dirons pas que B a été la cause de C.
Pourquoi? La réponse toute simple – et bonne, je crois – est que si Élodie n'avait pas jeté le caillou, il ne serait pas tombé sur la chaussée. Nous ne dirons pas la même chose de B: que si Élodie n'avait pas dit «potiron», le caillou ne serait pas tombé sur la chaussée46.
Mais que peuvent donc signifier ces affirmations? Il s'agit d'assertions contrefactuelles, c'est-à-dire qui parlent d'événements contraires aux faits. Dans le monde qui existe – le seul et unique, celui que nous avons noté MR dans la section 5 – Élodie a jeté le caillou, et a dit «potiron». Parler de ce qui serait arrivé si Élodie n'avait pas fait ces choses, c'est parler d'un monde qui n'existe pas. Que peut-on dire d'un monde qui n'existe pas?
On peut, bien entendu, l'imaginer. L'assertion «si Élodie n'avait pas jeté le caillou, il ne serait pas tombé sur la chaussée» se réfère à un monde que nous pouvons imaginer et où Élodie ne jette pas le caillou, et où celui-ci ne tombe pas sur la chaussée. Nous trouvons logique d'imaginer un tel monde; voire, nous lui donnons, en quelque sorte, un statut de réalité partielle, en considérant qu'est vraie l'assertion contrefactuelle «si... alors...».
Pouvons-nous faire de même pour l'autre assertion contrefactuelle, celle que nous rejetons: «si Élodie n'avait pas dit “potiron”, le caillou ne serait pas tombé sur la chaussée»? Bien entendu, nous devons sous-entendre «toutes choses égales par ailleurs», c'est-à-dire qu'Élodie jette le caillou (comme dans la réalité) mais s'abstient de dire «potiron».
Nous pouvons effectivement imaginer un tel monde, où le caillou, plutôt que de tomber sur la chaussée, flotte en l'air, par exemple, et revient tout seul se poser sur la table. Ce monde est parfaitement imaginable (vous venez de l'imaginer); cela suffit-il pour conclure que si Élodie n'avait pas dit «potiron», le caillou ne serait pas tombé sur la chaussée? Bien sûr que non.
Il ne suffit donc pas que nous puissions imaginer un monde alternatif où une assertion est vraie pour que nous considérions celle-ci comme vraie en tant qu'assertion contrefactuelle. Il faut encore que ce monde alternatif soit possible, au sens où j'ai utilisé ce terme dans ma description du modèle laplacien. Le monde imaginaire correspondant à la première assertion contrefactuelle est conforme aux lois de la physique, et en particulier, à la loi de la gravitation. Par contre, la seconde assertion contrefactuelle correspond à un monde où le caillou reste suspendu en l'air; ce monde est en contradiction avec les lois de la physique, et n'est qu'imaginable, mais non possible.
Cela suffit-il? Je ne le crois pas. Il faudrait pour cela pouvoir donner à la notion de loi physique elle-même un statut de réalité supérieur à celle du monde réel lui-même. Si le monde MR est tout ce qui existe, les lois physiques ne peuvent avoir un tel statut.
Que sont donc les lois physiques? Dans la perspective laplacienne, seul existe le monde MR. Celui-ci n'est cependant pas n'importe lequel: il est conforme à certaines lois physiques. Celles-ci nous apparaissent comme une collection de «régularités». Nous avons constaté dans le passé que chaque caillou, une fois lâché, tombe. Sans cette régularité, il nous faudrait, pour décrire MR, énumérer le comportement du caillou à chaque occurrence. Grâce à cette régularité, une seule phrase suffit.
De façon générale, les lois apparaissent dans le cadre laplacien comme l'expression de ce fait quelque peu «miraculeux» qui est que ce monde réel historique – cette succession d'une infinité de mondes instantanés – peut être «résumé» par la connaissance de n'importe lequel de ces mondes instantanés, plus quelques lois d'évolution relativement simples.
Cette conception des lois – la seule possible, me semble-t-il, dans le cadre laplacien – se heurte à trois difficultés, dont les deux premières ont été depuis longtemps reconnues:
– Comment se fait-il qu'un tel résumé est possible?
– Comment pouvons-nous, à partir du constat de ces régularités dans le passé, en déduire qu'il sera encore vérifié à l'avenir (problème de l'induction)?
– Si les lois ne sont que cela – le constat d'une régularité à l'intérieur de MR – elles ne constituent en aucune façon un discours relativement à d'autres mondes.
Je crois que ces trois difficultés sont liées, mais je laisse de côté les deux premières; la troisième suffit pour mon propos. Si la loi constate une régularité, et prévoit la répétition de la régularité à l'avenir, elle peut nous dire que lorsque le caillou aura été lâché par Élodie, dans le monde réel où elle dit en même temps «potiron», il tombera. Elle ne nous dit toujours rien à propos d'un autre monde, qui n'existe pas!
Nous voulons peut-être malgré tout considérer que ces lois peuvent nous parler de ces autres mondes en quelque sorte par extension. Un peu comme dire «puisque la moitié de tout nombre divisible par quatre est paire, si dix était divisible par quatre, cinq serait pair». Cependant, il se trouve qu'une même réalité – celle du monde réel MR – peut être décrite avec un grand nombre de jeux différents de lois. Nous pouvons aussi énoncer que «tout nombre divisible par quatre auquel on ôte cinq est impair»; en conséquence de quoi si dix était divisible par quatre, cinq serait impair! Il en va de même pour les lois physiques.
Par exemple, nous pouvons énoncer la loi suivante:
Chaque fois qu'une pierre est lâchée, elle tombe, sauf si les mots «556841278025 potirons» sont prononcés en même temps, auquel cas la pierre flotte.
Il se trouve que dans MR, ces mots exacts ne sont jamais prononcés au moment de lâcher une pierre; ou s'ils le sont (vous pouvez, maintenant que j'ai énoncé cette loi, la rendre fausse!), une infinité d'autres phrases du même genre ne le sont pas. Supposons donc, pour fixer les idées, que ce soit le cas pour celle-là. Cette loi est alors vraie. Par ailleurs, elle satisfait à tous les critères voulus de régularité. Elle a donc autant de validité en tant que loi décrivant MR que n'en a la loi habituelle, qui dit que la pierre tombera dans tous les cas.
Pourtant, la loi habituelle, et cette loi modifiée, sont en désaccord sur ce qui se serait passé si Élodie avait prononcé «556841278025 potirons» en lâchant la pierre: la loi habituelle prédit que la pierre tombera, la loi modifiée spécifie qu'elle flottera. Nous ne pouvons donc pas affirmer, sur la base des lois, ce qui se serait passé dans ce cas. Par conséquent, nous ne pouvons déterminer si le fait qu'Élodie n'ait pas prononcé cette phrase est, ou n'est pas, la cause de la chute du caillou.
On objectera peut-être que cette loi modifiée est plus compliquée que l'autre; que c'est la loi la plus simple qui «prévaut» (critère du «rasoir d'Ockham»). Je veux bien; mais en quel sens «prévaut»-elle? Ce critère est sans doute juste comme principe heuristique; il ne change pas pour autant le fait que ni la loi habituelle, ni la loi modifiée, ne peuvent être «testées» relativement à un monde qui n'existe pas, celui où la phrase serait prononcée; et seul ce monde-là est susceptible des les départager.
Dès lors, que reste-t-il? On peut se dire que peu importe ce qui serait arrivé si le monde avait été différent. Les lois régissent ce qui se passe dans le monde réel; ce qui se passerait dans un autre monde est pure affaire de convention. La cause d'une événement aussi; si A, B et C se sont produits, que ce soit A ou B la cause de C nous importe peu; ce qui nous importe, c'est qu'ils se sont produits!
Pouvons-nous accepter une telle conclusion? Je pense que non. La causalité fait partie des concepts fondamentaux de notre vie quotidienne, tout comme la notion de loi. Pour les tribunaux, par exemple, il n'est pas indifférent de savoir si c'est le geste de telle personne ou le mot prononcé par telle autre qui a fait tomber, mettons, un caillou sur le crâne du policier! Cette imputation de responsabilité que font les tribunaux n'est que la traduction du fait que chacun de nous – de nous, dirais-je, êtres sensibles, délibérants – décide de ses gestes en fonction de ses conséquences. Pour cela, nous devons croire en une causalité future au moment de la délibération.
Nous avons déjà noté une autre difficulté que rencontre la notion de causalité dans le modèle laplacien et qui tient à sa dissymétrie relativement au temps. La cause précède nécessairement l'effet; cela semble une règle absolue, voire définitionnelle, de la notion de cause. Or, nous avons vu que dans le modèle laplacien, le temps n'a pas de «flèche», c'est-à-dire que les mêmes lois restent vérifiées si l'on inverse le sens du temps. En particulier, si une «intelligence», comme disait Laplace, connaissait entièrement le présent, alors «l'avenir, comme le passé, serait présent à ses yeux». Cela semble suggérer que l'avant et l'après n'ont pas d'existence objective. Le déterminisme laplacien est tel que si le monde est, à l'instant t1, en un état instantané I1, en l'instant t2 il doit être en un certain état déterminé I2; en ce sens, on peut dire que l'état en l'instant t1détermine celui en l'instant t2. L'inverse cependant est tout aussi vrai: l'état en l'instant t2 détermine celui en l'instant t1; je n'ai d'ailleurs rien spécifié quant à l'ordre temporel de t1 et de t2.
Ce n'est pas dans un sens aussi pauvre que l'on entend généralement le concept de déterminisme. Par là nous pensons d'abord au fait que l'avenir est déterminé – entièrement déterminé – par le passé. Qu'il est causé par le passé. Le verbe «déterminer» est, dans le langage courant, presque synonyme de «causer»; et le déterminisme est souvent présenté comme une théorie de la causalité absolue. Nous avons vu que nous ne pouvons attribuer un tel sens au déterminisme laplacien; dans la vision laplacienne du monde, le monde est, tout simplement; rien n'est la cause de rien. Il est ironique que ce soit précisément dans ce cadre, perçu comme déterministe par excellence, que la notion de causalité perd son statut de réalité.
Cela est cependant logique, si on perçoit que dans la notion de déterminisme, ou de causalité, il y a un double aspect: celui de nécessité, et celui de liberté. «Déterminer que...», c'est aussi «choisir que...». Élodie détermine que le caillou tombera sur la chaussée par son geste de le jeter par la fenêtre; ce geste, elle pouvait s'abstenir de le faire. L'aspect de nécessité dans la notion de détermination est celle qui suit ce geste, et qui amène inexorablement le caillou à tomber. Sans cette nécessité-là, il n'y aurait pas de liberté de choix. Lorsque nous disons que le présent détermine l'avenir, et rechignons à envisager que ce puisse aussi être l'inverse, c'est parce que nous pensons pouvoir agir, au moins un peu, sur le présent, et par là modifier l'avenir. Nous ne pouvons agir directement sur l'avenir, et par là modifier le présent. Élodie ne peut faire directement que la pierre tombe dans dix secondes sur la chaussée, et par là amener sa main maintenant à jeter le caillou.
La raison pour laquelle le déterminisme laplacien dissout la causalité, et de ce fait ne représente plus qu'un déterminisme en un sens appauvri, tient justement au caractère absolu de son triomphe. Si tout est déterminé, plus rien ne peut déterminer.
En particulier, dans le déterminisme laplacien, nous sommes déterminés. On perçoit souvent le déterminisme comme contradictoire avec ce que traditionnellement on appelle le «libre-arbitre»; si «tout est écrit», on ne peut rien choisir. À l'encontre de cela, la tradition rationaliste répond souvent: tout est peut-être écrit (déterminé), mais comme nous ne savons pas ce qui est écrit, nous ne pouvons échapper à la nécessité de choisir, même si le résultat de ce choix pourrait être connu d'avance par une «intelligence» laplacienne. J'ai longtemps moi-même cru valable une telle réponse; aujourd'hui ce n'est plus le cas. Je pense au contraire qu'il y a, effectivement, une incompatibilité entre la notion de liberté et le déterminisme laplacien. Cela découle, cette fois encore, de la prise au sérieux du point de vue interne, et du principe de fondement par l'impossibilité de ne pas croire.
Dessert ou tofu?
Examinons encore une fois la situation délibérative. Prenons le cas où nous devons choisir entre ces deux possibilités: dessert ou tofu. Supposons vrai le déterminisme laplacien. Le choix que nous allons faire est alors déterminé par les conditions initiales, par la disposition des atomes dans notre cerveau. Mettons que ce soit dessert. Nous ne pouvons donc pas prendre tofu. Mieux, le terme «pouvoir» n'a pas de sens; dans le monde réel, le seul qui existe, nous prendrons dessert.
Pourtant, au moment où nous délibérons, nous avons pleinement la conviction de pouvoir prendre tofu, et de pouvoir prendre dessert. Tel est le fondement même de notre délibération. Ce n'est pas seulement que nous ne savons pas ce que nous prendrons. Supposons qu'on nous apprenne que de toutes façons, quoi que nous décidions de demander, le cuisinier n'en fera qu'à sa tête; il nous donnera le dessert ou le tofu, suivant ce qu'il a le plus en stock. Là encore nous ne savons pas ce que nous allons avoir, mais cette fois la délibération nous semble inutile. Ce n'est donc pas la seule incertitude qui fonde la délibération, mais le sentiment de pouvoir faire l'un des choix, ou l'autre.
Supposons maintenant que l'on nous apprenne que le cuisinier a déjà déterminé ce qu'il nous préparera, mais que cette fois il s'agit d'un cuisinier plus serviable. Lorsque nous sommes entrés au restaurant, il a entièrement scanné notre corps, et il connaît aussi, avec toute la précision nécessaire, l'environnement que constitue le restaurant. Par les lois du déterminisme laplacien, et à l'aide de son ordinateur personnel dernier cri, il a calculé que nous allions choisir dessert. Tout cela est tout à fait possible, en principe, dans le cadre du déterminisme laplacien.
Supposons maintenant que nous sachions tout cela; on nous apprend même que le choix que nous allons faire est écrit à l'intérieur d'un petit papier plié posé sur la table. L'avenir est vraiment écrit. Quelle logique y aurait-il alors à délibérer? Nous ne savons pas ce qui est écrit sur le bout de papier, mais nous savons que de toute façon nous n'allons pas le changer! Nous pouvons reposer notre esprit, et attendre d'être servis!
Cela est, dira-t-on, en contradiction avec nos prémisses: car le cuisinier a prévu que nous allions délibérer, et choisir dessert. Ses calculs laplaciens auraient dû au contraire lui indiquer que son client, informé de la présence et de la signification du petit papier sur la table, allait s'abstenir de délibérer. Dès lors, le cuisinier n'aurait pas su quel choix écrire sur le bout de papier!
Le problème est qu'il peut aboutir à la même conclusion concernant de chacun de nous, dès lors que nous croyons au déterminisme laplacien; et ceci, que l'avenir soit physiquement écrit ou non sur un bout de papier! Si nous croyons au déterminisme laplacien, nous n'avons aucune motivation pour délibérer. Nous délibérons pourtant. Je crois que cela signifie que nous ne croyons pas au déterminisme laplacien.
Je crois aussi que cela signifie que nous ne pouvons croire au déterminisme laplacien. Car nous ne pouvons que délibérer; même le choix de «reposer notre esprit» implique une délibération initiale.
La tentative que j'ai mentionnée de conciliation entre le déterminisme laplacien et la logique de l'individu délibérant n'opère que parce qu'elle refuse de prendre au sérieux le point de vue de celui-ci. La description de l'individu en termes de boules de billard possède sa cohérence interne. Mais dans cette description, il n'y a rien qui corresponde au fait de pouvoir faire un choix. Les boules de billard ne peuvent rien; elles font, c'est tout. Tout au plus pourrions nous trouver, si la sensibilité, les croyances, etc. étaient des «propriétés émergentes» d'un système laplacien, quelque chose au sein du tissu nerveux qui soit la croyance en notre possibilité de choix; mais trouver la croyance en une chose, ce n'est pas trouver la chose. Le point de vue laplacien peut être d'accord que nous croyons; il n'est pas d'accord avec ce que nous croyons. Il ne peut être le nôtre; nous ne pouvons le croire vrai.
Le paradoxe de Newcomb
Il s'agit là d'un paradoxe connu, formulé par le physicien William Newcomb en 196047. Je vais en donner une version légèrement modifiée, qui, partant de l'hypothèse du déterminisme laplacien, aboutit à une contradiction.
Nous allons cette fois encore supposer qu'il y a une «intelligence» laplacienne qui, munie de sa calculette, est capable de prévoir nos faits et gestes. Cette fois ce ne sera pas un cuisinier, mais un Zlork, venu de la Galaxie d'Andromède et qui propose une épreuve à une terrienne, appelons-la Noumène.
C'est une épreuve où Noumène ne peut que gagner, mais le montant de ses gains va dépendre de son choix.
Noumène est donc conduite dans une pièce où se trouvent deux boîtes fermées. Voici la règle de l'épreuve, qu'on lui explique. Chaque boîte contient une certaine somme d'argent. Noumène peut choisir d'emporter les deux ou de n'en emporter qu'une seule; elle ne les ouvrira qu'après avoir fait son choix. La somme d'argent contenue dans chaque boîte a été déterminée la veille au soir par le Zlork de la manière suivante:
— si le Zlork a prévu que Noumène allait prendre les deux boîtes, il a disposé dans chacune dix zlotys;
— si le Zlork a prévu que Noumène allait prendre une seule boîte, il a disposé dans chacune mille zlotys.
Le Zlork a fait cette prédiction la veille sur la base des informations acquises en scannant Noumène, ainsi que l'ensemble de l'environnement avec lequel elle allait entrer en contact entre-temps; y compris l'environnement auquel elle allait être exposée dans la pièce où a lieu l'épreuve. Il ne pouvait bien entendu pas tenir compte dans ces calculs du montant qu'allaient contenir les boîtes, puisque celui-ci dépend précisément du résultat des calculs; mais comme ce montant n'est pas communiqué à Noumène avant qu'elle ne ressorte de la pièce, son comportement ne peut pas en être affecté. Le Zlork dispose donc de la totalité des informations susceptibles de déterminer le comportement de Noumène, et peut donc, si le déterminisme laplacien est vrai et sa calculette suffisamment puissante, prévoir, avec certitude, ce comportement.
Si le déterminisme laplacien est vrai, tout cela est donc, au moins en principe, possible.
Noumène, en terrienne moyenne qu'elle est, veut emporter le maximum de zlotys. Elle connaît les règles du jeu. Que doit-elle choisir?
Réponse (1): elle a intérêt à prendre les deux boîtes. En effet, la somme qu'elles contiennent est déjà à l'intérieur; si elle prend les deux boîtes, elle empochera forcément deux fois plus que si elle n'en prend qu'une.
Réponse (2): elle a intérêt à ne prendre qu'une boîte. En effet, la boîte contiendra alors mille zlotys, puisque le Zlork aura prévu son comportement et y aura donc disposé cette somme; par contre, si elle prend les deux boîtes, chacune ne contiendra que dix zlotys, pour la même raison; elle ne gagnera donc que vingt zlotys, ce qui est nettement moins.
Je crois ces raisonnements tous deux irréfutables. Le premier est celui que Noumène ferait déjà dans les conditions banales où personne n'a prévu ses faits et gestes. Il se fonde sur une certaine causalité, limitée, où le choix de prendre une ou deux boîtes n'en modifie pas le contenu. Le second est dépendent du déterminisme laplacien; plus exactement, il est dépendent de la croyance de la part de Noumène en ce déterminisme. Il se fonde sur une autre causalité, par laquelle le choix de Noumène détermine le contenu des boîtes, en déterminant rétroactivement la somme qu'y a placée le Zlork!
Dans le cadre du déterminisme laplacien, il est impossible de départager ces deux causalités; seul existe le monde réel, unique, où tout se produit mais rien ne cause.
La contradiction à laquelle aboutit Noumène concerne deux assertions prescriptives: (1) «Prendre les deux boîtes!» et (2) «Prendre une seule boîte!». La contradiction disparaît, bien entendu, si nous refusons de considérer que les assertions prescriptives ont un sens réel; si ce ne sont que des illusions, la contradiction n'est qu'illusoire. Cette fois encore, c'est parce qu'il est impossible que nous ne croyions pas en la réalité de la signification des assertions prescriptives que nous devons rejeter les hypothèses permettant l'existence d'une telle contradiction. Plus spécifiquement, je pense qu'il est nécessaire de rejeter l'hypothèse selon laquelle il est possible, au moins en principe, pour un Zlork de prévoir, au moyen d'un ordinateur, ou par tout autre moyen, le choix que nous allons faire. Nous devons donc, pour le moins, rejeter le déterminisme laplacien, calculable.
Pourquoi Élodie ne saute pas par la fenêtre
Un troisième cas de figure montrera plus clairement la nécessité de croire en un certain caractère réel des mondes contrefactuels. Supposons encore Élodie au dernier étage d'un gratte-ciel. La fenêtre est ouverte. Élodie n'a aucune tendance suicidaire. Pourquoi ne saute-t-elle pas par la fenêtre?
La question est idiote, bien sûr: elle ne saute pas par la fenêtre parce que si elle sautait, elle tomberait et se tuerait.
Mais elle ne sautera pas, cela elle le sait. Quelle réalité peut-elle donc accorder à la phrase «si je sautais par la fenêtre, je tomberais»?
On retrouve là la contradiction déjà mentionnée concernant la cause de la chute du caillou; mais cette fois, il s'agit d'événements futurs, et non passés. Élodie est face au choix de sauter ou non; si elle ne saute pas, c'est parce qu'elle croit vraie la phrase «si je sautais, je tomberais». Si elle la croit vraie, c'est qu'elle décrit quelque chose de réel. Si pourtant le monde où Élodie saute n'est en aucune manière réel, cette phrase ne peut avoir de sens, ne peut être vraie.
La délibération est une situation où nous avons plusieurs possibilités. Nous devons croire à la réalité de ces possibilités, et aux conséquences qu'elles auront chacune, pour que notre délibération ait un sens. Cela implique de donner un réalité d'une certaine sorte à toutes ces situations futures. Cela est encore vrai dans des situations où notre choix est déjà fait, comme celui d'Élodie face à la fenêtre, dès lors que nous conservons la possibilité de choisir autrement. Élodie est libre de sauter, même si elle n'en a aucune intention. À cause de cette liberté, la situation où Élodie sautera garde une certaine réalité, et c'est cette réalité qui donne un sens à l'assertion à laquelle elle ne peut que croire: «Si je sautais, je tomberais.»
La situation délibérative qui est la nôtre implique donc de croire en notre liberté. Celle-ci est réelle même quand notre choix «coule de source». C'est cette liberté qui donne un sens à la situation délibérative, mais aussi à la causalité et aux lois.
Revenons à la situation d'Élodie avec sa pierre; mais supposons que le choix de son acte n'est pas encore fait. Elle peut choisir de lancer la pierre en disant «potiron»; de la lancer sans dire cela; de dire «potiron» sans lancer la pierre; enfin, de ne faire ni l'un ni l'autre. Si nous supposons que ces quatre mondes futurs possibles sont de quelque manière réels, c'est sans ambiguïté que nous pouvons affirmer que c'est le geste de lancer la pierre, et non le fait de dire «potiron», qui cause sa chute. En effet, dans les deux mondes où Élodie lance la pierre, celle-ci tombe, qu'elle dise ou non «potiron»; dans les deux autres, la pierre ne tombe pas.
Dès lors que les lois physiques ne sont pas cantonnées à une description d'un monde unique MR, mais sont contraintes par la nécessité de décrire une pluralité de mondes possibles, leur caractère arbitraire tombe. Puisque nous pouvons dire «556841278025 potirons», ainsi que toutes les phrases du même genre – même si nous n'avons aucune intention de le faire! – les mondes où nous prononçons ces phrases ont chacun une part de réalité; dans chacun de ces mondes, la pierre tombe (malgré notre phrase), et par conséquent aucune des lois modifiées que j'ai suggérées – où le fait de prononcer de telles phrases fait flotter la pierre – n'est vraie.
Le fantastique
J'ai conscience du caractère à la fois «fantastique» et mal défini de ces conclusions. Que peut donc signifier cette «réalité partielle»? Cette «pluralité de mondes»?
J'ai choisi de ne pas approfondir dans cet article la question de la mécanique quantique. Je me contenterai d'affirmer les points suivants, auxquels tout spécialiste du domaine souscrira:
Les postulats de la mécanique quantique possèdent, au regard du sens commun comme vis-à-vis de nos habitudes de pensée laplaciennes, un caractère tout à fait fantastique.
La mécanique quantique implique, ou au moins suggère fortement, l'existence possible d'une «pluralité de mondes»; qu'il s'agisse de la superposition quantique évanescente limitée au monde «microscopique», de la pluralité durable mais fragile du type «chat de Schrödinger», ou enfin de la multiplicité sans limites des théories à mondes multiples (Hugh Everett).
La contrefactualité possède en mécanique quantique un statut différent du (non-)statut qui est le sien dans la perspective laplacienne; dans certaines situations expérimentales, des assertions contrefactuelles paraissent même testables.
L'interprétation standard de la mécanique quantique (interprétation de Copenhague) vide de son sens la notion de réalité; si nous voulons reconstruire cette notion, il paraît envisageable que ce soit autrement qu'elle n'était conçue auparavant.
L'interprétation standard de la mécanique quantique fait jouer un rôle clé dans la levée de la superposition quantique à la notion d'observateur; notion non définie au sein de cette interprétation (ou définie implicitement comme étant un être humain), mais dont l'interprétation la plus immédiate en termes réalistes est celle d'une subjectivité. L'interprétation standard n'échappe à cette conclusion qu'en refusant la notion de réalité.
Je n'affirme certainement pas que la mécanique quantique, théorie non laplacienne (dans son interprétation standard) représente une solution au problème de l'existence de l'éthique, de la liberté et autres objets subjectifs. Au contraire, c'est en partant du subjectif que nous avons pu conclure à la nécessité de croire en l'existence d'une réalité, de «quelque chose»; existence que nie l'interprétation standard de la mécanique quantique. Celle-ci par ailleurs ne donne pas corps à une pluralité de mondes «durable». Enfin, l'interprétation en termes de mondes multiples, celle qui semblerait le mieux convenir à certaines de nos conclusions, représente un retour à une conception laplacienne; nous avons vu que cela ne convient justement pas48.
Nous pouvons envisager les points énumérés ci-dessus plutôt comme des indices dans une enquête policière; comme des éléments suggérant que nous sommes sur une bonne piste, sans que nous sachions encore les assembler en un tableau d'ensemble.
Penrose, de son côté, ne croit pas du tout à l'interprétation des mondes multiples. Par contre, il a individualisé au sein du tissu nerveux certaines structures très particulières – les microtubules – susceptibles, selon lui, de maintenir la cohérence quantique (entre «mondes multiples») suffisamment longtemps pour que certains phénomènes, qu'il suppose déterministes mais non calculables, puissent opérer49. Ce seraient ces phénomènes, liés à la gravitation quantique, qui produiraient la «réduction de la fonction d'onde» et donc, en quelque sorte, un choix non calculable du monde futur réel parmi les divers possibles. Or, si notre situation délibérative est celle qui implique de donner un sens à une pluralité des mondes futurs, c'est aussi elle qui choisit parmi ces mondes.
Là encore, il s'agit de considérations qui ne constituent même pas l'amorce d'une théorie achevée et satisfaisante. Cependant, elles suggèrent au moins ceci: il se pourrait que certaines caractéristiques du subjectif fassent partie des lois fondamentales de la physique, le tissu nerveux représentant un lieu privilégié d'utilisation de ces lois dans le sens d'une résolution efficace des problèmes auxquels un organisme doit faire face pour survivre, et que la subjectivité proprement dite, avec ses qualia, ses plaisirs et ses douleurs, résulte de cette utilisation.
7. La réalité de la sensibilité
(...) remarquant que cette vérité: Je pense, donc je suis, était si ferme et si assurée que toutes les plus extravagantes suppositions des Sceptiques n'étaient pas capables de l'ébranler, je jugeai que je pouvais la recevoir sans scrupule pour le premier principe de la philosophie que je cherchais50.
Si dans cette démarche cartésienne nous substituons la simple perception à l'acte de penser, nous pouvons argumenter que notre propre caractère d'être sensible est une évidence première; et que par conséquent la sensibilité elle-même existe comme fait du monde. Cette sensibilité qui se constate elle-même est cependant en quelque sorte autistique; Descartes est ensuite obligé de faire appel à l'idée de Dieu pour tenter de démontrer l'existence du monde lui-même.
Nous avons vu (section 4) que toute action, toute délibération, est foncièrement altruiste, en ce sens qu'elle ne se préoccupe pas de ce que ressent la sensibilité au moment même de la délibération, mais se projette sur les conséquences de l'acte, nécessairement futures, non perçues, mais prévues, supposées. Descartes part de l'évidence de ce qui est directement perçu. Je propose une autre voie, qui part de l'impossibilité de ne pas croire à certaines choses non directement perçues.
En effet, nous avons vu que nous ne pouvons pas ne pas croire que cela a un sens de nous demander «Que faire?»; et que dès lors, nous ne pouvons pas ne pas croire en la vérité en soi des réponses que nous cherchons, qui sont de la forme «Faire telle chose!». Enfin, si cela a un sens de chercher de telles réponses, c'est nécessairement que ces réponses sont vraies en vertu de critères ou de règles qui peuvent nous être accessibles. S'il nous était a priori impossible de déterminer la bonne réponse, il n'y aurait pas de sens à la chercher.
La souris dans la bûche
Pour fixer encore plus les idées, supposons que j'aie fait un feu de bois en plein air, et que je m'apprête à y ajouter une bûche. Je remarque qu'il y a une cavité dans la bûche, et qu'au fond de la cavité est terrée une souris. J'ai une deuxième bûche à ma disposition, mais elle est maculée de boue, et je préfère éviter de me salir les doigts. J'envisage donc de mettre au feu la première bûche, celle où se terre une souris.
J'en fais part aux amis qui m'entourent, et je recueille trois réactions:
1. Romain me dit: ce n'est qu'une souris, donc un corps dépourvu d'âme; nous le savons parce que l'on n'a jamais vu de souris parler. Elle ne ressent donc rien, et si elle crie en grillant, ce sera comme le crissement du bois; tu dois donc préférer cette bûche à l'autre. Ce choix est moins cruel envers la souris qu'il n'est doux envers tes doigts, à qui il évitera de se souiller51.
2. Pierre me dit: c'est une souris qui possède un système nerveux, un cerveau, comme nous, et qui peut donc ressentir la souffrance; elle souffrira terriblement si tu la mets au feu. Prends donc l'autre bûche, même si cela doit te salir les doigts.
3. Édouard me dit: d'après notre propre expérience, nous savons chacun que nous pouvons souffrir, et par analogie nous le savons des autres humains. Mais se demander jusqu'où, en descendant l'échelle des espèces animales, il y a encore quelque forme de sensibilité, cela relève de la spéculation gratuite; ce sont des questions auxquelles on ne peut pas apporter de réponse et qui doivent être laissées à des rêveurs désœuvrés. Cela n'a donc pas de sens de nous demander si la souris peut souffrir. Par conséquent, tu as raison de choisir cette bûche plutôt que l'autre, et de garder les mains propres.
Romain et Pierre admettent tous deux que la sensibilité ou non-sensibilité de la souris est de l'ordre du fait. Ils pensent tous deux aussi que ce fait est déterminant pour la réponse à «Que faire?». Leur différence réside dans un désaccord sur ce fait lui-même.
Tous deux pensent aussi avoir abouti à leur conclusion sur la (non-)sensibilité de la souris à partir d'un raisonnement, portant sur des données. Celles-ci sont de l'ordre du factuel, au sens classique: l'absence de parole chez les souris, la présence d'un tissu nerveux, etc.
Édouard, par contre, ne conclut ni que la souris est sensible, ni qu'elle ne l'est pas; il estime cette question dépourvue de sens. «Par conséquent», dit-il, nous pouvons faire comme si elle ne l'était pas.
Il y a là un raisonnement fréquemment tenu, mais qui est en réalité un non-raisonnement. Du fait qu'une certaine assertion A («la souris est sensible») est (selon lui) dépourvue de sens, Édouard conclut que nous devons agir comme si elle était fausse.
Pourtant, si une assertion est dépourvue de sens, il doit en être de même de sa négation. Le même raisonnement, s'il est valable, implique donc que nous devons agir aussi comme si non-A était faux; et par conséquent, comme si l'assertion A était vraie.
À vrai dire, Édouard, je crois, a raison: si A est dépourvu de sens, nous devons agir comme si A était vrai, et aussi comme si A était faux. Seulement, comme je vais l'expliquer, il est impossible d'agir en satisfaisant ces deux conditions. Il s'ensuit que, contrairement à ce qu'affirme Édouard, A n'est pas dépourvu de sens. La souris est, ou n'est pas, sensible.
Que sont donc ces assertions dépourvues de sens? Je pense qu'on peut en dire au moins ceci: une assertion est dépourvue de sens si on peut la supposer vraie ou fausse, sans que cela ne change réellement le monde. Si A est dépourvu de sens, un monde où A est vrai et un autre où A est faux sont en réalité le même monde. Les assertions normales, non dépourvues de sens, je les appellerai par contre «assertions substantielles».
Supposons qu'une assertion dépourvue de sens implique une autre assertion qui, elle, est substantielle. Cela ne peut pas arriver, voudra-t-on peut-être dire. Pourtant, Édouard admettait tout comme Romain et Pierre que si la souris était sensible, il ne faudrait pas la brûler; c'est parce que cela n'a pas de sens de dire qu'elle est sensible qu'il conclut qu'on peut la brûler. Il admet donc que A («la souris est sensible») implique B («il ne faut pas brûler la souris»), tout en pensant que A n'a pas de sens, et que l'on ne peut donc conclure B.
Cependant, si nous admettons ma conclusion selon laquelle les assertions prescriptives ont un sens, sont donc substantielles, l'assertion B, de caractère prescriptif («il ne faut pas brûler la souris»), est substantielle.
Si A est dépourvu de sens, nous pouvons l'imaginer faux, ou vrai, sans que cela ne change réellement le monde. Mais dans la «version» du monde où A est vrai, nous devons aussi supposer B vrai, puisque A ⇒ B. Dans l'autre «version» du monde, où A est faux, B doit être vrai aussi, puisqu'il s'agit en fait du même monde, et que B est une assertion substantielle.
En somme, si une assertion dépourvue de sens implique une assertion substantielle, celle-ci est nécessairement vraie.
Comme déjà indiqué, si A est dépourvu de sens, il en va de même de non-A. Par conséquent, nous pouvons dire:
Toute conclusion substantielle qui découlerait soit de la vérité soit de la fausseté d'une assertion dépourvue de sens est vraie.
En l'occurrence, cependant, nous avons A ⇒ B, mais aussi non-A ⇒ non-B; nous devons conclure que B est à la fois vrai et faux, c'est-à-dire que nous ne devons pas brûler la souris, et que nous devons la brûler. Si nous croyons au caractère substantiel des assertions prescriptives, il est impossible que nous ayons une telle contradiction. Il s'ensuit que notre hypothèse ne peut être vraie: il ne peut être vrai que A est dépourvu de sens. Le fait que la souris soit ou non sensible est donc un fait substantiel, un fait réel du monde.
Cela vaut pour les souris, mais aussi, bien entendu, pour tout autre animal; et même, pour tout système matériel enfermé dans la bûche. Cela a un sens de nous demander si les bactéries, le bois ou les cailloux incrustés dans la bûche sont sensibles; la réponse est peut-être qu'évidemment non, mais elle ne peut être que la question n'a pas de sens.
Égoïsme et non-hédonisme
Pour parvenir à cette conclusion, j'ai supposé que la bonne réponse à la question «Que faire?» dépend du plaisir ou de la souffrance éventuels que notre choix occasionnera. Plus précisément, il m'a fallu supposer qu'elle dépend du plaisir et de la souffrance éventuels occasionnés chez la souris. Il y a cependant a priori deux autres possibilités:
– que la bonne réponse ne dépende que de mon propre plaisir ou souffrance éventuels (hypothèse égoïste);
– que la bonne réponse ne dépende du plaisir et de la souffrance de personne (hypothèse non-hédoniste52).
Examinons d'abord l'hypothèse égoïste. Comme je l'ai déjà noté, le «moi-même» envers qui cette éthique manifeste sa sollicitude est forcément un «moi-même» futur. Si nous refaisons notre raisonnement «souris» avec ce moi-même futur à la place de la souris, nous aboutissons tout de même à cette conclusion: cela a un sens de supposer existante une sensibilité qui m'est pourtant, de fait, étrangère. Telle est, en effet, la sensibilité de ce moi-même futur; il s'agit d'une sensibilité que je n'éprouve pas, ni n'ai jamais éprouvée, dont je ne constate pas l'existence plus que je ne constate l'existence de la sensibilité d'autrui.
Le seul soutien que je connaisse du solipsisme est le caractère problématique de l'altérité, de l'existence d'une autre sensibilité que la mienne. Par définition, une sensibilité est ressentie; comment puis-je croire à l'existence d'une sensibilité que je ne ressens pas? Mais ce raisonnement ne peut s'arrêter là, puisqu'il en va de même de ma propre sensibilité future. Si le problème de l'altérité doit nous pousser au solipsisme, ce doit être jusqu'au solipsisme instantané, qui considère comme inexistante toute sensibilité autre que la mienne présente.
Or c'est là précisément une conclusion que nous ne pouvons accepter, dès lors que nous admettons qu'il y a nécessairement une réponse juste à la question «Que faire?» , et que celle-ci dépend de quelque plaisir ou souffrance occasionnés; même si elle ne dépend que de «mon» plaisir ou souffrance futurs. Le solipsisme instantané ne peut donc être juste. Malgré son caractère problématique, l'altérité existe, et cette conclusion retire son principal fondement au solipsisme en général.
Il en va de même de la logique qui fonde cette thèse fréquemment émise de l'impossibilité radicale d'un véritable altruisme, et qui tient dans la question: faire souffrir un autre, qu'est-ce que cela peut me faire? La réponse, évidemment, est «rien», sauf dans la mesure où cette souffrance peut rejaillir sur mon propre bien-être, auquel cas nous retrouvons une motivation égoïste. Cependant, cette même question se pose relativement à toute préoccupation pour ma propre souffrance: ma souffrance de demain (ou de dans cinq minutes), que peut-elle donc me faire à moi maintenant? La réponse, là encore, est «rien», un «rien» absolu, cette fois, dans la mesure où l'effet ne peut précéder la cause. Cette logique qui devrait justifier l'égoïsme (voire rendre impossible l'altruisme) impliquerait que rien ne peut être une motivation juste pour mes choix; et à cela nous avons vu que nous ne pouvons croire.
À l'inverse, dès lors que nous nous rendons compte de l'absence d'une perception directe de notre ressenti futur par notre ressenti présent, ce ressenti futur de nous-même se retrouve dans un même rapport avec notre ressenti présent que le ressenti de n'importe quel autre individu: un rapport d'altérité complète. Si, malgré cette altérité, notre plaisir et malheur futurs sont une motivation juste pour nos choix présents, il n'y a pas de raison pour qu'il n'en soit pas de même pour le plaisir et le malheur futurs d'autrui.
Je n'ai sans doute pas à proprement parler démontré la fausseté de l'hypothèse égoïste, mais seulement retiré son fondement, et montré que sa vérité ne changerait pas foncièrement ma conclusion: que cela a un sens de supposer l'existence objective d'une sensibilité autre que celle que nous percevons au moment de la délibération.
Il nous reste enfin à envisager l'hypothèse non-hédoniste, qui est que la motivation juste pour mes actes puisse ne dépendre du plaisir et de la souffrance de personne. Remarquons d'abord qu'il s'agit d'une hypothèse à laquelle, de fait, nous ne croyons pas, et à laquelle à mon avis personne n'a jamais cru. Elle impliquerait que la douleur n'est en aucune façon une motivation juste pour tenter de la faire cesser; que le malaise éprouvé si nous cessons de respirer n'est aucunement une motivation juste pour continuer à le faire. C'est pourtant, depuis la naissance, pour ces raisons-là, d'abord, que nous nous protégeons de la douleur; et que, sans doute, nos ancêtres font de même depuis des millions d'années, ainsi que tous les êtres sensibles qui se protègent de la douleur et de la souffrance. Croire en cette hypothèse n'impliquerait pas forcément de cesser de respirer53; la respiration pourrait continuer à être l'acte juste pour d'autres raisons. Mais cela serait en quelque sorte une coïncidence; croire en cette hypothèse impliquerait donc d'être prêt à cesser de respirer si ces autres raisons venaient simplement à disparaître, quelles que soient les souffrances de l'asphyxie, lesquelles ne compteraient pour rien comme motivation.
En disant cela, je n'ai pas démontré ni que la douleur et le plaisir sont les motivations justes pour nos actes, ni qu'il s'agirait là d'une assertion à laquelle nous ne pouvons que croire. Peut-être cependant peut-on prendre le problème à l'envers. Nous avons vu que ne pouvons pas ne pas croire que la question «Que faire?» a un sens, et que la recherche de la réponse juste a un sens, et enfin que les critères et règles pour déterminer cette réponse ne peuvent a priori être hors de notre portée. Il faut donc bien qu'il y ait quelque chose qui puisse constituer un but pour nos actes. Ce quelque chose doit aussi nous apparaître comme un but en soi, et non un moyen pour atteindre un autre but. Or c'est précisément ainsi que nous apparaissent la souffrance et le plaisir: comme, de manière immédiate, des choses à éviter ou à rechercher.
Il ne serait pas juste de vouloir définir la souffrance et le plaisir comme les termes négatif et positif immédiats de nos finalités; ce serait vouloir donner une définition en quelque sorte opérationnelle à des objets qui existent en soi. Le raisonnement est plutôt qu'il doit exister quelque chose comme une motivation primaire, et que d'autre part nous constatons que la souffrance et le plaisir sont cette motivation primaire.
Il est bon ici de rappeler que la souffrance et le plaisir que nous ressentons à un certain moment ne constituent pas à proprement parler la motivation qui guide notre délibération à ce même moment, puisque celle-ci ne peut avoir d'effet que sur une souffrance et un plaisir futurs. Ils constituent plutôt un «échantillon» de cette souffrance et ce plaisir autres; ils nous les font connaître, en somme. Il est juste par ailleurs d'affirmer que nous avons une connaissance directe de notre propre sensibilité immédiate; mais s'il n'y avait que cela, rien ne nous interdirait de nous enfermer dans le solipsisme instantané. C'est la situation délibérative à laquelle nous ne pouvons échapper qui implique que nous sortions de nous-mêmes, que nous croyions en l'existence (au moins possible) de sensibilités autres, et aussi, que nous croyions possible pour nous d'en déterminer l'existence, et d'agir sur elles.
C'est donc la situation délibérative qui implique que nous croyions en un monde «extérieur», en une réalité objective. Au sein de celle-ci existent nécessairement des relations causales, «mécaniques», faute desquelles nous n'aurions aucune possibilité d'agir; et existent aussi, en tant qu'entités tout aussi objectives, des subjectivités, reliées dans un sens comme dans l'autre au monde «matériel», «mécanique», faute de quoi nous ne pourrions les connaître et agir sur elles. Ou plutôt: ces subjectivités font partie du monde «matériel», font partie du même monde physique, même si nous ne savons pas encore aujourd'hui les repérer exactement et comprendre leurs interactions avec le reste du monde physique.
Sensibilité et situation délibérative
J'ai soutenu que nous sommes placés dans la situation délibérative, et que cela fait de nous des êtres éthiques (des agents moraux), et des êtres libres (doués de libre-arbitre). Nous sommes aussi des êtres sensibles. Peut-on affirmer que tout être sensible est dans la situation délibérative, et que réciproquement tout être dans la situation délibérative est sensible?
Sur la base des développements précédents, je crois très plausible d'affirmer que tout être délibératif doit aussi être sensible. Croire semble bien être une sensation. De plus, la délibération implique une motivation primaire; nous avons vu que c'est la souffrance et le plaisir qui jouent ce rôle chez nous. Si quelque chose d'autre jouait ce rôle chez un autre être – mettons, une zouffrance et un blaisir – il semble que cela ne devrait faire aucune différence dans son comportement; il nous supplierait de le préserver de la zouffrance, et/ou de lui accorder le blaisir, sans même peut-être que ces «choses» ne soient perçues (s'il n'est pas un être sensible, mais seulement délibérant). Nous nous retrouverions dans la situation d'impossibilité radicale de déterminer le caractère sensible de l'être, impossibilité radicale à laquelle nous ne pouvons pas croire.
Je crois que la réciproque est vraisemblable aussi. Il me semble que la souffrance a toujours la valeur d'une motivation primaire pour la faire cesser, et que l'existence d'une telle motivation n'a de sens que si elle s'insère dans un processus délibératif.
On pourrait imaginer une sensibilité qui ne perçoive aucune souffrance ni aucun plaisir; qui ne perçoive que des qualia neutres, comme des couleurs, des textures, des sons, qui ne lui fassent ni plaisir ni déplaisir. Dès lors, elle prendrait connaissance de la réalité, mais ne connaîtrait pas de motivation pour délibérer ni agir. Il me semble cependant que la connaissance de la réalité n'a de sens pour nous que par nos possibilités d'action sur elle; une telle situation est peut-être temporairement possible, mais je doute qu'elle corresponde à un état durable où serait placé un être réel quel qu'il soit.
Il ne faudrait pas croire cependant qu'il soit possible d'établir une relation simple, quantitative et fiable entre les capacités d'action d'un être et son degré de sensibilité. Nous pouvons être paralysés – sous l'effet de certaines substances, par exemple, ou encore dans un cauchemar – tout en éprouvant une souffrance intense. Cela n'implique pas que nous ne délibérions pas; seulement, cette délibération ne débouche, de fait, sur rien.
Je pense néanmoins que très généralement, les êtres sensibles – même les insectes et les vers de terre, s'ils sont sensibles – sont dans la situation délibérative, et par conséquent, sont des agents éthiques, au moins dans un sens minimal.
8. Réalité et virtualité
Notre culture technophile tend de plus en plus à diffuser comme une évidence l'idée d'un caractère purement logique de la réalité, et de l'équivalence entre le virtuel et le réel. J'ai parlé (section 5) du mythe du robot pensant prédit par Turing. Un exemple plus moderne est celui de la série de films Matrix, où les personnages (si j'ai bien compris) ne parviennent pas eux-mêmes à déterminer s'ils sont réels ou au contraire ne résultent que de l'exécution de quelque sous-programme dans un ordinateur géant. Pourtant ils souffrent, désirent, luttent. Le discours implicite est que puisque toute réalité peut être simulée par un programme – et les réalisations modernes de simulation de paysages, d'avions, de textures et ainsi de suite sont souvent saisissantes – la perception subjective elle-même peut être simulée, et devient de ce fait quasi-réelle, impossible à distinguer d'une subjectivité réelle.
La «souffrance virtuelle» est-elle vraiment équivalente à la souffrance réelle? Fait-elle mal?
Je crois que la réponse est oui et non: oui, en ce sens que la souffrance virtuelle, si elle existait, serait effectivement équivalente à la souffrance réelle, en vertu du rejet de l'épiphénoménisme (section 5). Elle serait équivalente en un sens éthique: nous aurions la même obligation morale de la faire cesser. Mais cela nous mènerait, nous le verrons, à une situation absurde. Par conséquent, la souffrance virtuelle ne peut exister.
Mais que sont donc ces choses «virtuelles»? Nous avons vu (section 5) que dans la perspective laplacienne, la totalité du monde peut à chaque instant être décrite par un ensemble de nombres, et que son évolution, à partir de cette description, est soumise à un déterminisme calculable, c'est-à-dire peut être prévue par l'application d'un algorithme. Cela est vrai du monde dans sa totalité, du moins en théorie; cela est vrai aussi de n'importe quelle partie du monde. Si je connais à un instant t1 l'état complet d'un être humain, par exemple, c'est-à-dire, pour reprendre notre image, l'état de chacune des boules de billard qui le composent, je peux calculer dans quel état il sera (ou était) à n'importe quel autre instant t2, à condition cependant d'ajouter une information supplémentaire: je dois connaître aussi l'ensemble des influences extérieures ayant pu affecter le système dans l'intervalle de temps [t1, t2]. S'agissant d'un être humain, je dois connaître l'ensemble des interactions verbales ou autres qu'il a pu avoir avec d'autres humains, l'ensemble des choses qu'il a vues et ainsi de suite; mais il ne suffit pas que j'en connaisse simplement la teneur générale, il faut que je connaisse ces interactions molécule par molécule, boule de billard par boule de billard.
Moyennant ces conditions, peu vraisemblables s'agissant d'un système aussi complexe qu'un être humain mais possibles à remplir en principe, le calcul qui permettra de connaître l'état du système en t2 à partir de son état en t1 sera une simulation. L'ordinateur contiendra au départ dans sa mémoire une représentation binaire de chacun des nombres décrivant le système; cet ensemble de représentations binaires formera un modèle du système simulé. Le calcul se fera pas à pas, en appliquant les lois d'évolution sur des intervalles de temps très petits; plus ils seront petits, plus la précision du calcul sera grande. À chaque pas, donc, le modèle sera la représentation du système à un certain instant; au bout d'un certain nombre de pas, il représentera le système en t2.
Cette simulation consiste donc en l'existence d'une correspondance entre chacune des parties du système réel et une contrepartie dans le modèle. À chaque boule de billard correspond un ensemble de six représentations numériques, décrivant ses trois paramètres de position et ses trois paramètres de vitesse. N'importe quel groupement de boules de billard correspond aussi à un ensemble de représentations numériques; n'importe quelle relation entre boules de billard correspond à une relation entre représentations numériques. Aux intervalles de temps élémentaires du système réel correspondent les pas de calcul qui font évoluer le modèle. En définitive, toute caractéristique du système réel a son correspondant «virtuel» au sein du modèle qui le simule; et ceci, même lorsqu'il s'agit d'une caractéristique non instantanée, mettant en relation des états du système à des instants différents.
Si le monde est laplacien, la sensibilité est forcément le produit de certaines relations entre les «boules de billard» – molécules, champs, etc. – à l'intérieur de notre cerveau. Si notre cerveau est simulé par un modèle tel que nous l'avons décrit, ce qui est toujours en principe possible (si le monde est laplacien), cette sensibilité a elle aussi son correspondant virtuel au sein de ce modèle. Si l'être humain souffre, le modèle «éprouve» au «même moment» (au stade correspondant dans le déroulement de l'algorithme) une «souffrance virtuelle».
Telle est donc la notion de souffrance virtuelle. Nous nous sommes demandé si une telle souffrance est équivalente à une souffrance réelle; nous pouvons reformuler cette question, en accord avec la caractérisation de la souffrance introduite en section 7: une telle souffrance virtuelle constitue-t-elle une motivation primaire dans nos délibérations? Avons-nous une obligation morale de la faire cesser?
Les positions A, B, C et D de Penrose
Penrose distingue sur la question du statut physique de la sensibilité les quatre positions suivantes:
A: Toute pensée est algorithmique; en particulier, les sensations de perception consciente apparaissent par le simple fait d'exécuter l'algorithme approprié.
B: La conscience est une propriété des actions physiques du cerveau; mais bien que toute action physique puisse être simulée algorithmiquement, une simulation algorithmique ne peut par elle-même faire apparaître une conscience.
C: Certaines actions physiques particulières dans le cerveau induisent la conscience, mais ces actions ne peuvent pas être simulées par un algorithme.
D: La conscience ne peut être expliquée en des termes physiques ou algorithmiques ou de quelque manière scientifique que ce soit.
D est la position mystique; je crois que nous pouvons l'écarter, puisqu'elle implique l'impossibilité a priori de déterminer par des moyens physiques – les seuls à notre disposition – si un objet donné est ou non conscient, et donc l'impossibilité de trouver une réponse à la question «Que faire?».
Dans le cadre d'une conception laplacienne du monde, nous avons le choix entre les positions A et B. Toutes deux admettent en effet la possibilité de la simulation algorithmique de notre cerveau, possibilité qui découle, on l'a vu, de la conception laplacienne. Elles diffèrent par la réponse qu'elles donnent à notre question sur l'équivalence entre une souffrance virtuelle et une souffrance réelle; A y répond positivement, B négativement. A est la position dite d'«intelligence artificielle forte»; c'est celle qui fut admise implicitement par Turing (voir section 5). B par contraste représente la position d'«intelligence artificielle faible», et rejette la position opérationnaliste sur la subjectivité, aussi bien en tant que définition qu'en tant que critère. Elle suppose qu'un ordinateur peut exister qui réussirait pleinement au test de Turing, mais cet ordinateur ne serait pas réellement sensible.
La position C est en contradiction avec la conception laplacienne. C'est celle de Penrose lui-même, qui envisage par conséquent la possibilité d'un déterminisme non calculable (voir section 5). C'est aussi ma propre position.
J'ai expliqué dans la section 6 les raisons pour lesquelles je crois le déterminisme laplacien incompatible avec la situation délibérative. Penrose donne d'autres arguments à l'encontre du déterminisme calculable, arguments fondés sur le théorème de Gödel et que je vais rapidement résumer. J'y ajouterai une argumentation spécifique à l'encontre de A, argumentation qui rejoint certaines remarques de Penrose et de Searle, et qui a trait au caractère arbitraire de la relation entre le modèle et le système qu'il simule. Enfin, je ferai valoir à l'encontre de la position B le fait qu'elle paraît impliquer l'épiphénoménisme.
La conclusion sera l'impossibilité de la simulation algorithmique d'au moins certains phénomènes physiques. Je soutiendrai enfin qu'il me semble probable que de tels phénomènes physiques ne sont en fait simulables ni algorithmiquement, ni d'aucune autre manière; c'est-à-dire qu'il n'est pas possible, en général, de prendre la copie complète d'un système physique.
L'argumentation de Penrose
Penrose développe dans les deux ouvrages que j'ai cités une argumentation à l'encontre de la possibilité de simuler tout particulièrement les capacités humaines de pensée mathématique. Il le fait sur la base d'une forme modifiée du théorème de Gödel. Je renvoie à ces ouvrages pour un exposé complet de ses thèses, incluant la réponse à un grand nombre d'objections qui lui ont été faites. Je vais me contenter d'en tracer les grandes lignes.
Le célèbre théorème de Gödel (1931) porte sur la possibilité d'une formalisation complète du raisonnement mathématique. La conclusion de son théorème est qu'une telle formalisation n'est pas possible. Penrose s'appuie sur une variante de ce théorème en termes algorithmiques.
Le cerveau humain est capable de démontrer des théorèmes mathématiques. Si le monde est laplacien, tout ce qui s'y déroule peut être simulé par un algorithme. Cet algorithme sera alors un algorithme démonstrateur de théorèmes.
Qu'est-ce que cela signifie? Nous allons supposer que nous pouvons en donner la caractéristique suivante. Un algorithme A «démonstrateur de théorèmes» sera tel que:
– A opère sur une classe infinie de problèmes mathématiques. Il peut s'agir d'une classe repérée par un nombre. Un exemple de telle classe peut être: «Existe-t-il un nombre premier supérieur au nombre entier n?» L'algorithme A prend comme valeur d'entrée le nombre n, et soit nous donne une réponse, soit ne nous répond jamais (poursuit son calcul sans jamais aboutir à un état final).
– Nous savons, du fait de notre compréhension mathématique, que A est sûr, en ce sens que lorsqu'il nous donne une réponse, cette réponse est toujours vraie. Nous n'exigeons pas qu'il nous donne toujours une réponse. Pour reprendre l'exemple précédent, il pourra s'agir de l'algorithme suivant, décrit en langage libre: «tester si n + 1 est premier; si oui, donner la réponse “oui”; sinon, tester le nombre suivant, et ainsi de suite». Du fait de la structure de cet algorithme, nous voyons bien que s'il nous répond, la réponse sera nécessairement juste. De façon générale, ce sera notre compréhension mathématique de la structure de A qui nous permet de voir (de démontrer) que A est sûr.
Penrose suppose que A agit sur une classe très générale de problèmes mathématiques, qui sont eux-mêmes de la forme: «Tel algorithme, appliqué à tel nombre, aboutit-il ou non à un état final?».
Par une forme modifiée du théorème de Gödel (due à Turing), Penrose nous montre54 que nous pouvons construire un algorithme G appliqué à un certain nombre dont nous pouvons démontrer qu'il aboutit à un état final, mais qui est tel que A ne donne pas de réponse le concernant.
La conclusion de Penrose est qu'un tel algorithme A ne peut englober l'ensemble des capacités humaines de résolution de cette classe de problèmes, ou que s'il le fait, nous ne pouvons le savoir, ou ne pouvons savoir qu'il est sûr. Car si nous le savons, et savons que A est sûr, nous pouvons immédiatement construire l'algorithme G pour lequel nous connaissons la réponse, mais pour lequel A ne peut donner la réponse.
Cette conclusion elle-même découle de manière assez immédiate du théorème de Gödel, et n'est contestée par personne55. Ce qui est contesté – par les tenants de l'intelligence artificielle forte, en particulier, est la volonté de Penrose d'en conclure qu'aucun algorithme A ne peut englober l'ensemble de notre compréhension mathématique. L'objection au raisonnement de Penrose est que notre compréhension mathématique peut très bien être englobée dans un tel algorithme, sans que cet algorithme puisse être connu (par nous) comme étant sûr; et qu'il n'est, d'ailleurs, pas sûr. Nous savons en effet que les humains peuvent se tromper, y compris dans leurs raisonnements mathématiques.
Il n'est cependant pas sans conséquences d'admettre que la compréhension mathématique humaine puisse se tromper, non du simple fait de notre distraction, mais dans son principe. Cela implique qu'il doit exister quelque théorème comportant une erreur de raisonnement, mais qui est par ailleurs tel que nous sommes incapables, y compris en principe (par l'application de l'algorithme qui fonde notre raisonnement mathématique), de percevoir cette erreur; nous déclarerons vrai, avec certitude, le résultat édicté par ce théorème alors qu'il est faux. Penrose note56:
Mais est-il vraiment plausible d'affirmer que nos convictions mathématiques inattaquables puissent se baser sur un système de déduction non sûr – si peu sûr, en fait, que «1 = 2» fait partie, en principe, de ces convictions? Certainement, si nous ne pouvons nous fier à notre raisonnement mathématique, alors nous ne pouvons nous fier à aucun de nos raisonnements concernant la structure du monde. Car le raisonnement mathématique forme une part essentielle de toute notre compréhension scientifique.
L'argumentation de Penrose57 se conclut ainsi par une question rhétorique à laquelle il nous suggère de répondre «non», sans pourtant proposer de justification rigoureuse. Je crois cette argumentation correcte en substance, et susceptible d'être fondée de manière plus solide sur la base de la nécessité de prendre au sérieux le point de vue interne, nécessité qui m'a servi de fil conducteur tout au long du présent article, et qui, je crois, se trouve en filigrane dans bien des raisonnements de Penrose lui-même. Je ne développerai pas plus ce point ici, faute de place et de temps.
Je pense utile cependant de noter que ce qui semble en jeu dans l'ensemble de ce raisonnement, c'est le caractère substantiel de la compréhension mathématique. L'algorithme «démonstrateur de théorèmes» ne démontre, ni même n'affirme, rien en lui-même; il ne démontre des théorèmes que parce que notre jugement mathématique indépendant le perçoit, par l'examen de sa structure, comme sûr. Dès lors que nous faisons des mathématiques, nous ne pouvons pas ne pas croire que notre perception mathématique est celle d'une vérité indépendante de nos assertions; si nous supposons qu'elle n'est en réalité que l'exécution d'un algorithme, donc d'un processus incapable, par lui-même, d'affirmer quelque chose au sujet de la vérité, l'ensemble de notre compréhension mathématique perd tout sens. Je ne crois pas qu'il soit réellement possible, donc, que nous croyions que nos perceptions mathématiques résultent de l'exécution d'un algorithme.
Ce que je trouve remarquable dans l'approche de Penrose est qu'elle s'appuie sur la compréhension mathématique, faculté souvent perçue comme reflétant par excellence la rationalité spécifiquement humaine, pour soutenir le caractère substantiel de toute compréhension. Le mathématicien et le ver de terre se retrouvent mis, fondamentalement, sur le même plan; l'un et l'autre perçoivent, comprennent, et participent, essentiellement, de la même situation dans le monde.
Penrose nous parle peu d'éthique. La question animale est cependant présente dans ses écrits; il prend soin de noter, dans chacun des deux ouvrages que j'ai cités, qu'il ne croit nullement que la sensibilité soit limitée à l'espèce humaine58, et semble prêt à en tirer quelques conséquences éthiques.
Algorithmie et contrefactualité
Je vais revenir sur cette question de relation entre algorithme et sensibilité sous un autre angle, celui du caractère abstrait de l'algorithme. Penrose consacre plusieurs pages à cette question59 en rapport avec l'argumentation de John Searle sur la «chambre chinoise60». Je vais développer ici cette thématique à ma propre façon.
La position A implique que l'exécution d'un algorithme est capable, de son seul fait, d'induire des sensations subjectives. Il s'agit ici de sensations réelles, et non d'une simple apparence de sensations, d'un comportement extérieur (piloté par les résultats du calcul) qui serait «comme si» la machine exécutant l'algorithme était sensible, sans qu'elle ne le soit vraiment (position B).
Pourtant, un algorithme n'est lui-même qu'un objet mathématique abstrait; à ce titre, il n'a aucune localisation ni dans le temps ni dans l'espace. Comment peut-il dès lors engendrer une sensation, objet physique réel?
En fait, A ne postule pas que l'algorithme lui-même engendre des sensations; c'est l'exécution de l'algorithme qui est censée avoir cet effet61. Nous devons alors nous demander: qu'est-ce qui compte comme exécution d'un algorithme?
Le cas classique d'exécution d'un algorithme est celui que peut effectuer un ordinateur. L'algorithme est représenté dans la mémoire de l'ordinateur comme un programme, sous la forme de tensions et de charges électriques dans cette mémoire; il en est de même des données sur lesquelles cet algorithme opère. Ces données forment une représentation concrète de notre modèle de la réalité.
Par le jeu des lois physiques gouvernant les circuits électriques qui constituent l'ordinateur, ces données seront transformées pas à pas de la manière spécifiée par l'algorithme. C'est ce processus physique qui constitue l'exécution de l'algorithme.
Il est parfaitement possible, cependant, de voir ce même processus physique d'une autre manière: comme un simple jeu sans signification de lois de l'électronique, comme des heurts de boules de billard, qui, partant d'une certaine configuration initiale, aboutissent au bout d'un certain temps à une autre configuration. Voir en ce processus l'exécution d'un algorithme implique d'ajouter un sens à ce déroulement physique.
Ce sens est d'abord celui qui fait d'une certaine configuration de tensions électriques la représentation du modèle, c'est-à-dire de nombres. Mais cette relation, c'est nous qui l'établissons! La représentation courante d'un nombre dans un ordinateur se fait par une série de circuits électroniques capables de prendre deux états stables. Nous appelons un de ces états «0» et l'autre «1». Nous convenons qu'une certaine collection de, mettons, 64 de ces mémoires binaires dispersées parfois aux quatre coins de l'ordinateur représente, dans un ordre fixé lui aussi par convention, l'écriture binaire d'un certain nombre parmi tous ceux qui forment le modèle.
En somme, le contenu de l'ordinateur, sans des conventions arbitraires que nous établissons, ne représente rien du tout. Cela contredit le caractère réel, et non conventionnel, de la souffrance et du plaisir qu'est censée induire l'exécution de l'algorithme.
On dira peut-être que c'est le programme lui-même qui «force» une certaine interprétation des états de mémoire de l'ordinateur en termes de nombres. Par exemple, lors de l'opération d'addition de deux nombres, la retenue binaire est propagée dans un certain ordre entre les différentes mémoires binaires; c'est cet ordre qui fixe celui de l'interprétation de ces mémoires binaires en tant que nombre.
Je ne crois pas que cette objection suffise. Le programme peut peut-être fixer une interprétation comme étant la plus «raisonnable». D'autres interprétations restent toujours possibles. Nous pouvons interpréter la collection de 64 mémoires binaires dans n'importe quel ordre, quitte à ce que l'opération effectuée sur ces nombres soit d'un caractère absurde. Le processus d'exécution ne sera sans doute alors la représentation d'aucun processus physique; il correspondra cependant encore à l'exécution d'un algorithme, qui ne sera pas l'algorithme initial que nous voulions voir exécuter, mais un autre, inutile. Le problème du caractère arbitraire de la relation entre la représentation et le nombre représenté n'est pas résolu.
La même chose peut être dite du statut du programme codé lui aussi par des mémoires binaires, et censé représenter l'algorithme. Mais il y a un autre problème concernant cette représentation de l'algorithme. L'exécution concrète, qui est censée induire des sensations, se fait nécessairement sur un jeu de données de départ. Or un algorithme, en tant qu'objet mathématique abstrait, est capable d'opérer sur une pluralité de jeux de données de départ; en principe, même, sur une infinité. Par exemple, l'algorithme d'addition de deux nombres dans leur représentation décimale est capable d'additionner n'importe quel jeu de deux nombres parmi l'ensemble infini des couples de nombres entiers. C'est ce caractère infini des valeurs possibles pour les données de départ qui constitue l'algorithme en tant que représentation d'une certaine logique. Un algorithme capable seulement d'additionner deux et deux peut s'énoncer simplement par l'instruction «imprimer quatre»; rien ne le distingue d'un algorithme de multiplication limité lui aussi aux mêmes données. Il n'incorpore aucune logique d'addition. Tout algorithme capable d'opérer seulement sur un ensemble fini de données est équivalent à l'énumération finie des résultats de cette opération, énumération qui n'incorpore aucune logique générale.
Or, comme je l'ai dit, l'exécution concrète d'un algorithme par un ordinateur part d'un seul jeu de données de départ. On dira peut-être: oui, mais cette exécution se fait suivant des lois de la physique qui la rendent possible sur n'importe quel jeu de données de départ; ce sont ces lois qui instituent le programme en mémoire comme représentation de l'algorithme.
Nous retrouvons là le problème de la contrefactualité: le processus concret est l'exécution de l'algorithme en vertu, non de lui-même, mais de ce qui se passerait aussi dans d'autres mondes que le monde réel!
Pour rendre ce problème plus concret, supposons un ordinateur en train d'exécuter un certain algorithme sur un certain jeu de données de départ D. Supposons que cet algorithme et ces données sont tels que cette exécution engendre, en vertu de A, certaines sensations. Supposons un deuxième ordinateur identique, exécutant le même algorithme sur le même jeu D, à ceci près que nous avons ajouté un petit dispositif extérieur mesurant les données entrant dans le microprocesseur, et une plaque chauffante par-dessous. Ce dispositif extérieur est organisé de manière telle que s'il voyait entrer dans le microprocesseur d'autres valeurs que celles de D, il allumerait la plaque chauffante, laquelle fondrait le microprocesseur. Il se déclencherait ainsi dans un autre monde que le monde réel; dans le monde réel, il n'interfère en rien avec l'exécution de l'algorithme.
Pourtant, parce que le système complet ordinateur + dispositif extérieur ne pourrait exécuter l'algorithme sur d'autres données que D, il n'exécute plus réellement cet algorithme. Par conséquent, en vertu d'un dispositif extérieur qui n'interfère en aucune manière avec ce qui se passe concrètement dans l'ordinateur (puisqu'il ne se déclenche pas), ce deuxième ordinateur n'engendre plus les sensations qu'engendrait le premier.
Il semble donc que le fait qu'un certain dispositif engendre certaines sensations dépende, non de ce qui se passe dans le monde réel, mais de ce qui se passerait dans d'autres mondes que le monde réel...
Ce n'est là qu'une des conséquences étonnantes, et en fait incroyables, qui découlent du caractère abstrait d'un algorithme et du caractère arbitraire de la correspondance entre la représentation des données dans une machine et ces données elles-mêmes. Sans entrer dans les détails, il me semble probable que l'assertion suivante soit vraie: dans un monde laplacien, tout processus physique quel qu'il soit, se déroulant à n'importe quel moment, peut, moyennant des règles de correspondance adéquates, représenter l'exécution de n'importe quel algorithme sur n'importe quel jeu de données. Il en découlerait que, suivant les règles de correspondance que nous choisissons d'envisager, la souffrance et le plaisir, ainsi que n'importe quelle sensation, seraient n'importe où, n'importe quand.
Il me semble clair, donc, que si A était vrai, la finalité de réduire la souffrance et d'augmenter le plaisir ne pourrait avoir aucun sens. Cela viderait de sens la situation délibérative, à laquelle nous ne pouvons pourtant pas ne pas accorder un sens. Par conséquent, nous ne pouvons croire que A soit vrai.
La position B et l'épiphénoménisme
La position B se place elle aussi dans le cadre laplacien, et suppose donc possible la simulation algorithmique de n'importe quel phénomène, et donc, en particulier, celle du cerveau entier d'un être sensible. Elle postule cependant, contrairement à A, qu'une telle simulation n'engendrerait pas les sensations dont est le siège le système simulé. La sensibilité est liée non à l'exécution d'un algorithme, mais à cette exécution au sein d'un certain type de matière.
Telle est la position de Searle, lequel n'explique pourtant pas de quelle nature pourrait être ce lien. Cette thèse a l'avantage de ne pas faire découler la sensibilité de cet objet abstrait qu'est l'algorithme, mais de l'objet concret au sein duquel l'algorithme est exécuté. La simulation informatique d'un ouragan, dit Penrose (à la suite de Searle), n'est certainement pas elle-même un ouragan62.
Il me semble que cette position implique assez directement l'épiphénoménisme (que j'ai défini dans la section 5), et doit donc être rejetée. En effet, la sensibilité est présente dans le système simulé, mais absente dans le système simulant. Le résultat de l'évolution du système simulant ne peut donc être causé par une sensibilité. Supposons par exemple que l'ordinateur simulant un être humain soit placé dans le crâne d'un robot androïde, et que le résultat de son exécution actionne les organes moteurs du robot, de manière à lui donner le même comportement que l'être humain simulé. Si celui-ci crie de douleur, l'androïde criera, mais sans douleur; ce sera pourtant le même cri. Chez l'être humain, à moins de supposer vraie la thèse épiphénoméniste, la douleur est la cause du cri; du moins, elle participe à sa détermination. Chez l'androïde, aucune douleur n'est la cause du cri. Celui-ci sera entièrement déterminé par l'exécution de l'algorithme sur les données modélisant le cerveau humain; le rapport de causalité entre le cri et ces données est le même que le rapport de causalité entre le cri de l'humain et les paramètres que représentent ces données au sein de son cerveau, à savoir la position et la vitesse des différentes boules de billard. La douleur, absente chez l'androïde, semble superflue chez l'être humain, semble s'ajouter à un rapport causal déjà complet; il ne lui reste rien à causer. Nous retrouvons donc la situation épiphénoménale.
Peut-on simuler tout système physique?
La conclusion est donc qu'un système physique sensible ne peut être simulé de manière algorithmique; car nous avons soutenu à l'encontre de A qu'une telle simulation ne peut être sensible, et à l'encontre de B qu'elle doit l'être.
Si cette conclusion est vraie, elle implique que la physique ne peut être laplacienne.
Penrose cherche, de manière spéculative, à développer une physique non laplacienne, où entrerait en jeu un déterminisme non calculable. A priori on peut imaginer qu'au sein d'une telle physique, la simulation d'un système par un autre resterait possible, à condition que le système simulant un système soumis à un déterminisme non calculable soit lui-même déterminé de manière non calculable; ce ne pourrait être, en particulier, un ordinateur.
Dans la section 6 j'ai montré que la possibilité de simuler un être sensible conduisait à une contradiction, en particulier dans le cadre du paradoxe de Newcomb. J'avais supposé que cette simulation se fasse par ordinateur; en réalité, pourtant, le caractère algorithmique de la simulation n'intervenait pas. Ma conclusion, si elle est valable, implique l'impossibilité de toute simulation d'un être sensible.
Mon raisonnement à propos du paradoxe de Newcomb était liée à l'impossibilité de ne pas croire en notre propre liberté. Il me semble que le problème que nous pose la définition même du libre-arbitre est pour une part au moins due à l'habitude invétérée et largement inconsciente que nous avons de supposer que tout système physique peut, nécessairement, être simulé par un autre. Si nous admettons que ce n'est pas le cas, nous pouvons peut-être conserver le déterminisme – au moins une certaine forme de déterminisme non calculable – sans pour autant qu'il soit possible d'acquérir à un certain instant la totalité de l'information définissant un système pour «rejouer» son évolution ailleurs. Nos décisions libres pourraient garder leur caractère d'unicité et d'imprévisibilité, sans pour autant n'être déterminées par rien.
Il est remarquable que cette conclusion elle aussi «dit quelque chose» à toute personne connaissant la structure de la mécanique quantique. Celle-ci en effet rend elle aussi impossible, dans le cas général, la mesure complète d'un système pour le reproduire à l'identique sans détruire le système original. Comme je l'ai déjà indiqué à la fin de la section 6, je n'affirme pas pour autant que la mécanique quantique, telle qu'elle existe, constitue la solution à notre problème, et ne vois dans cette convergence qu'un indice du fait que nous sommes peut-être sur la bonne voie.
9. Conclure un peu
Cet article est de loin le plus long que j'aie jamais écrit, et celui dont la rédaction m'a demandé le plus d'efforts. La difficulté principale pour moi a été le sentiment d'aborder un domaine peu reconnu, particulièrement en France, de faire face à des certitudes contradictoires mais fortement ancrées, et de devoir développer des considérations qui ne cadrent avec aucun registre discursif établi. Les militants préfèrent ordinairement des idées à efficacité immédiate. Les philosophes, pour la plupart, savent peu de choses de la physique, et la considèrent a priori comme non pertinente dans leur domaine. Les physiciens, symétriquement, méprisent toute philosophie, surtout si elle prétend avoir des implications concernant leur propre spécialité. Il m'a fallu défendre un point de vue – le mien – en rupture avec l'orthodoxie de chacun de ces domaines, du fait de son réalisme éthique, et aussi, paradoxalement, de son réalisme physique.
Je n'aurais jamais développé ces considérations si je n'avais découvert, il y a trois ans, l'œuvre de Roger Penrose; et si l'équipe des Cahiers n'avait apporté son soutien actif et patient au projet de numéro thématique sur ce sujet. Une de mes craintes majeures a été, et reste, l'accusation de «mysticisme» qui ne manquera d'être lancée à l'encontre de mes thèses. Je crois utile d'expliquer plus bas pourquoi je crois une telle imputation infondée.
Je voudrais cependant d'abord rassembler les quelques conclusions pratiques qu'il me semble pouvoir tirer d'ors et déjà des thèses que j'ai développées; conclusions qui, je crois, ne peuvent être fondées autrement que par des considérations en rupture avec les conceptions physiques et philosophiques dominantes.
La sensibilité: quels critères?
À vrai dire, les critères de sensibilité que l'on peut dégager de mes thèses ne diffèrent guère de ceux que nous suggère l'intuition. Quelle est alors l'utilité pratique de tous ces développements? Elle réside, comme indiqué dans la section 1, dans l'espoir de mieux fonder ces critères. Car nous n'écoutons notre intuition que si nous le voulons bien; nous avons vu que de larges secteurs de la population ne le veulent pas bien, et oscillent entre l'attribution opportune d'une sensibilité aux carottes voire aux cailloux – pour mieux pouvoir déclarer que tout étant dans tout, on ne peut rien en conclure – et la restriction tout aussi opportune de la sensibilité à la seule espèce humaine.
Le simple fait de parvenir à parler de la sensibilité sans le sentiment que tout discours sur ce sujet doit nécessairement conduire à une impasse sur le plan scientifique, ou dissoudre cette question dans un fonctionnalisme dépendant de l'arbitraire des descriptions humaines ou d'une téléologie naturelle – l'un et l'autre peu susceptibles de fonder une prise en compte éthique sérieuse – me semble à même d'affermir nos discours lorsque nous affirmons que oui, les cochons et les poules sont sensibles, et que non, il n'est pas plausible que les carottes le soient, et qu'enfin, si nous ne savons aujourd'hui dire si et à quel point les insectes le sont, nous le saurons peut-être un jour, et qu'en tout cas, la question a bel et bien un sens, puisqu'elle a un sens éthique.
Un premier critère que nous pouvons mettre en avant est celui de l'intelligence. Je crois que l'intelligence – la capacité de comprendre le monde – est nécessairement liée, au moins au niveau évolutionnaire, à la sensibilité. Cette affirmation est à la fois conforme à notre intuition et étonnante au regard des thèses habituelles de l'antispécisme. Un être plus intelligent mérite-t-il plus de considération pour ses intérêts? Assurément non; c'est la sensibilité, et non l'intelligence, qui justifie de prendre en compte les intérêts d'un être; ou plutôt, qui fait qu'un être a des intérêts à prendre en compte. Il n'est cependant pas contradictoire avec cette position d'affirmer qu'une corrélation existe entre l'intelligence et la sensibilité.
L'intelligence, capacité de comprendre le monde, n'est pas une caractéristique spécifiquement humaine. Elle constitue un ingrédient obligatoire de la situation délibérative. Si les décisions pouvaient être prises par un pèse-pulsions à trois neurones, il n'y aurait aucun besoin d'une souffrance ou d'un plaisir, aucun besoin d'une délibération, aucun besoin d'une compréhension du monde. Je pense que la situation délibérative met en jeu des mécanismes non algorithmiquement déterministes, dont l'issue ne peut être prévue «mécaniquement». Or, c'est bien le débat autour du caractère «mécanique» ou non des animaux qui a été, historiquement, et qui reste dans bien des discours, synonyme de débat sur leur sensibilité. S'ils ne sont que des machines, nous a dit Descartes, alors ils ne sentent pas; leurs cris ne sont pas causés par une souffrance et par une tentative d'agir sur le monde pour faire cesser cette souffrance, mais seulement par le déroulement inexorable, infiniment reproductible et prévisible d'une mécanique d'horloge. À l'inverse, la capacité à «innover» semble caractéristique de la situation délibérative; et nous avons vu que celle-ci implique très probablement la sensibilité.
Un certain discours sur les plantes tend à leur attribuer une sensibilité du simple fait qu'elles réagissent parfois à la prédation en «communiquant» à d'autres plantes, au moyen d'un gaz (l'éthylène), la nécessité de se protéger. De fait, cette «communication» peut s'expliquer par des mécanismes parfaitement automatiques, n'impliquant jamais une situation délibérative; on ne peut donc y voir l'indice d'une sensibilité.
L'intelligence d'un système peut certainement être plus ou moins grande; je pense qu'il en est de même pour la sensibilité. Il n'est pas dit cependant que la corrélation entre les deux soit directe ni constante. Surtout, en l'absence d'une compréhension plus précise tant de l'intelligence que de la sensibilité, nous n'avons aucun moyen un tant soit peu précis pour mesurer ni l'une ni l'autre. Je ne crois pas absurde, cependant, de supposer qu'une mouche puisse être sensible, mais moins qu'un humain ou un éléphant adultes.
Concernant cette question du «plus» et du «moins» de la sensibilité, je pense que nous devrons admettre que notre conscience n'est pas un tout; ou qu'au moins elle l'est moins que nous ne tendons à le penser. Les cas de «cerveau divisé» – où la communication entre les deux hémisphères du cerveau a été interrompue – incitent à penser qu'il peut peut-être arriver, par exemple, qu'un hémisphère soit heureux et l'autre triste. Si la souffrance du tout – des deux hémisphères ensemble – compte éthiquement pour 1, la souffrance de chaque hémisphère doit bien compter pour 1/2. En tout cas, nous pouvons espérer pouvoir un jour quantifier la souffrance et le bonheur, lorsque nous comprendrons mieux ces phénomènes. Là encore, cependant, il faut se garder d'un schématisme qui voudrait qu'un cerveau plus grand souffre plus qu'un cerveau plus petit!
Certainement en corrélation avec l'intelligence et la situation délibérative en général, donc avec la sensibilité, sont les capacités d'action. Une plante ne peut rien contre un prédateur; si à chaque morsure elle souffrait, cette souffrance serait vaine. Elle inciterait la plante à délibérer; mais cette délibération ne pourrait jamais déboucher sur rien. Il est bon de noter que la délibération, chez les seuls êtres dont nous sachions qu'ils délibèrent – chez les animaux, donc, dans leur tissu nerveux – est grande consommatrice d'énergie, de cette énergie qui est très généralement, pour la vie, le facteur limitant. Utiliser les «muscles du cerveau» est fatigant, et nous évitons de le faire gratuitement. On peut soupçonner que la délibération implique, par nature, une grande consommation d'énergie. Il est peu probable que l'évolution développe un tel phénomène s'il n'a aucune utilité en termes de survie et de reproduction.
Un raisonnement évolutionnaire ne peut cependant avoir un caractère absolu. Une caractéristique peut très bien subsister en tant que vestige chez un organisme après être devenue inutile voire nuisible. Je pense par exemple aux moules et aux huîtres; elles possèdent un tissu nerveux, et appartiennent à un embranchement dont certains membres (poulpes...) sont assurément sensibles et fort intelligents. Chez elles, la sensibilité est peut-être inutile; leurs capacités d'action semblent limitées à l'ouverture et à la fermeture de leur coquille en fonction de facteurs externes simples (immersion, température...). Il est cependant possible que dans leur cas la sensibilité n'ait pas régressé au point de disparaître.
Je crois intéressant d'envisager, justement, la sensibilité dans le cadre de l'évolution. La souffrance, dit-on souvent, est un «simple» mécanisme inventé par l'évolution pour provoquer un comportement d'évitement, par exemple. Une certaine vision du darwinisme, dite adaptationniste, réduit en définitive toute caractéristique d'un organisme à sa seule fonction, indépendamment des conditions de sa possibilité. Pourtant, les ailes des oiseaux ne se réduisent pas à leur utilité pour échapper aux prédateurs; elles sont aussi dues à des phénomènes spécifiquement physiques, comme la portance de l'air, qui rendent possible le vol. Si l'air était moins massif, par exemple, les ailes devraient être plus grandes pour effectuer le même travail; leur développement n'aurait peut-être pas «valu le coup» en termes évolutifs.
La souffrance et le plaisir sont très certainement des mécanismes augmentant la survie et la reproduction des organismes! Je propose cependant d'envisager que la sensibilité, ainsi que l'intelligence – la possibilité de la délibération non algorithmiquement déterminée – aient pu représenter, un peu comme le vol, des possibilités offertes par la physique; les mécanismes de l'évolution auraient «profité» de ces possibilités, tout en restant dépendants de la physique qui les sous-tend. La sensibilité et la situation délibérative ne sont donc pas de «simples» mécanismes mis en place par l'évolution, mais des phénomènes physiques à part entière, possédant leurs propres contraintes.
Une de ces contraintes est peut-être le coût énergétique, que j'ai déjà noté. On peut aussi remarquer la lenteur de nos pensées. Ce n'est pas une caractéristique du tissu nerveux en général; qu'on songe à la vitesse à laquelle nous intégrons les innombrables informations visuelles représentant un visage ou un paysage pour en reconnaître presque instantanément les éléments. Mais il s'agit là d'opérations automatiques, inconscientes. Pourtant, dès que nous cherchons à comprendre le sens d'une phrase même simple, mais présentant un caractère nouveau pour nous – par exemple une proposition mathématique peu familière – il nous faut des secondes, voire des semaines. Nous comprenons et pensons lentement. S'il était possible de le faire très vite, on peut supposer que l'évolution y aurait pourvu.
Cette lenteur est peut-être en rapport avec les considérations que Penrose développe sur certaines structures au sein de certaines cellules nerveuses, et qui pourraient être le siège de phénomènes quantiques impliquant un temps d'action minimal. Ces considérations semblent aussi suggérer que ce sont bien certains types de tissus, et non d'autres, qui peuvent être le siège d'une sensibilité; le candidat évident est, bien sûr, le tissu nerveux. Il est certainement faux d'affirmer que tout tissu nerveux est le siège d'une sensibilité; il est peut-être bien vrai par contre que seul ce tissu, et éventuellement d'autres reconnaissables par la possession de structures analogues, peuvent être sensibles.
Ces considérations sont-elles mystiques?
Si le mysticisme consiste à mettre le doigt sur des questions auxquelles nous ne savons pas répondre, j'avoue que mes thèses ici sont mystiques. Je crois bon de noter cependant que je n'affirme en aucune manière l'impossibilité de répondre un jour à ces questions; au contraire, mes efforts ont visé à cesser de prendre la sensibilité pour un phénomène surnaturel et à commencer à créer les conditions pour la saisir dans le cadre d'une compréhension unifiée du monde.
Si je m'étais contenté d'exposer d'un côté les dogmes de la physique moderne, lesquels pourtant nient la possibilité même d'attribuer au cailloux et aux sentiments une réalité en soi, et d'autre part quelque conviction religieuse catholique ou autre, j'aurais nettement moins encouru le reproche de mysticisme. Il est tout à fait vrai que je parle d'esprit, si on considère ce mot comme synonyme de «sensibilité». Mon «mysticisme» tient surtout au fait que j'en parle hors des cadres reconnus, qui permettent de l'isoler hermétiquement du monde des cailloux.
Enfin, mes considérations sont tout à fait dépourvues d'une des caractéristiques habituelles de ce qu'on désigne généralement comme mysticisme, à savoir le holisme. Je ne crois pas l'«esprit» susceptible d'être rassemblé en un grand tout. Au contraire: la sensibilité me semble plutôt divisible. A l'inverse, une collection d'êtres sensibles et délibératifs se comporte souvent d'une manière tout à fait mécanique. Rien de plus prévisible et mécanique qu'une foule, en bien des circonstances où, pourtant, chaque individu reste un être intelligent et libre. Si je crois en la sensibilité, et en sa présence potentielle en toute matière, je ne crois pas en un grand esprit de l'univers, en un dieu, en somme. Je ne crois pas l'univers mû par un but. Tout au plus puis-je penser que peut-être une tendance présente en tous les êtres sensibles peut les amener, progressivement, à harmoniser leurs intérêts, leurs actes et leurs désirs.
Retour sur l'impossibilité de ne pas croire
Je voudrais revenir sur ce principe que j'ai utilisé plusieurs fois dans cet article, celui du «fondement par l'impossibilité de ne pas croire». Je le crois susceptible de nous aider à sortir de quelques impasses de la philosophie et de la physique. On peut cependant facilement le percevoir comme une forme de renoncement. Si nous ne pouvons démontrer une chose, mais que du fait de notre situation nous ne pouvons qu'y croire, autant nous y résigner, dira-t-on; en pratique, cela revient au même, mais nous resterons insatisfaits. Une part plus élevée de nous, la part idéaliste, voudrait ne croire que par raison.
Je ne pense pas qu'une telle position soit justifiée. La philosophie a voulu que tout puisse être fondé sur la raison. C'est assurément là une bonne chose, lorsque cela nous évite des erreurs. Mais, dira-t-on, ce n'est pas pour éviter les erreurs que l'on est philosophe; c'est parce qu'on aime la raison pour elle-même!
Il y a là comme un aveu: l'amour de la raison, ce n'est pas que l'amour de la vérité. La vérité peut avoir une portée pratique immédiate; la raison, elle, n'a de portée pratique que dans la mesure où elle nous permet d'atteindre la vérité. Pourquoi donc serait-on amoureux de la raison, plutôt que de la simple vérité?
Je crois que cette passion pour la raison «pour elle-même» est une façon de nous projeter hors du monde. Nous voudrions être ailleurs, dans un ailleurs où nous serions purs esprits, où rien ne se corrompra, où nous ne mourrons pas comme meurent et pourrissent les bêtes. Pour ne pas pourrir, nous voulons être cette chose sans substance, la raison. Et en même temps que nous nous désincarnons nous-mêmes, nous désincarnons le monde, le réduisons à un jeu de billard insensé. Telle est la partition platonicienne, chrétienne, et enfin cartésienne du monde, celle du spécisme absolu: les humains et les cailloux, morts, en définitive, les uns comme les autres.
Prendre acte du fait que nous croyons ce que nous ne pouvons pas ne pas croire, ce n'est pas renoncer; c'est accepter notre situation dans le monde, celle qui fait que nous existons. Nous pensons et ressentons, mais ne sommes que de la matière, comme les cailloux, les bactéries, les mouches et les cochons. Que nous ressentions, et que les cailloux ne ressentent pas, cela reste à expliquer; mais nous ne sommes pas d'une autre substance qu'eux. Nous sommes dans le monde autant qu'eux, nous constituons le monde comme eux.
S'il faut être amoureux d'une notion, à la raison je préfère la vérité. Ce désir de vérité, je le crois pleinement satisfait si nous acceptons mon principe.
Supposons que Morganne croie vraie une proposition A; et qu'en même temps elle sache qu'elle le croit. Son désir de vérité sera-t-il satisfait? La réponse est oui; car les conditions de satisfaction de ce désir sont purement subjectives. Que A soit, de fait, vrai ou faux, du point de vue de Morganne cela revient au même. Dès lors qu'elle a la certitude (même erronée) de la vérité de A, et qu'elle sait qu'elle a cette certitude (d'une chose dont elle a la certitude qu'elle est vraie), elle ne peut être que satisfaite.
Ce raisonnement semblera peut-être cynique; Morganne est satisfaite tout en étant peut-être dans l'erreur. Mais s'agissant des choses que nous ne pouvons pas ne pas croire en raison de notre situation d'êtres sensibles et délibérants, ce point de vue extérieur n'existe pas. Concernant ces choses, ni nous-mêmes ni personne ne croit Morganne dans l'erreur. Je ne vois pas ce que l'on peut demander de plus!
Gwenva
Gwenva est mort il y a bientôt un an. C'était un chat, comme on peut le remarquer sur la figure 1 qui orne le début de cet article.
Il a été photographié au milieu d'une expérience de physique. Son regard fasciné me fascine; il essaye de comprendre le monde. Il a la conviction qu'il peut en comprendre quelque chose, et qu'en même temps quelque chose lui échappe; il pense que le monde existe par lui-même. Il a en cela raison, je crois, à l'encontre de bon nombre des fondateurs de la mécanique quantique.
Il croit aux lois de la physique. Sa patte est levée, hésitante; il se sait libre de frapper le filet d'eau, ou de ne pas le frapper; il pourra percevoir l'effet de son choix, dans un cas comme dans l'autre. Il croit à sa liberté, et il croit à la causalité. Il croit aussi en la réalité du plaisir de vivre et d'apprendre, y compris chez un modeste chat non humain.
Gwenva le physicien croyait en toutes ces choses auxquelles notre physique et notre philosophie ne voudraient pas que nous croyions. Pas bête, ce Gwenva!
* Sensibilité, ou sentience. Au moment de l'écriture de cet article, le terme «sentience» n'avait pas encore été introduit en français. Voir Estiva Reus, «Sentience!».
1. Les qualia (singulier: un quale) sont les caractéristiques purement subjectives des sensations; c'est «l'effet que cela me fait» d'avoir la sensation de rouge, par exemple, «effet» qui se distingue de ce que cela me fait de voir du vert. Le terme date de 1929 (C.I. Lewis) et est principalement utilisé chez les anglo-saxons.
2. Les Ombres de l'esprit: à la recherche d'une science de la conscience, éd. InterÉditions, 1995 (trad. de Shadows of the Mind, 1994); voir aussi L'Esprit, l'Ordinateur et les Lois de la physique, éd. InterÉditions, 1992 (trad. de The Emperor's New Mind, 1989). Ne possédant que les éditions en anglais, j'indiquerai pour les références à ces ouvrages les numéros de chapitre et de section plutôt que de page.
3. La Libération animale, éd. Grasset, 1993, pp. 40 à 47.
4. Ibid., p. 352.
5. Joan Dunayer, «Les poissons: une sensibilité hors de portée du pêcheur», Cahiers antispécistes n°1, octobre 1991.
6. Erwin Schrödinger, L'Esprit et la Matière, trad. Michel Bitbol, Seuil, 1990, p. 154; original en anglais Mind and Matter, 1958.
7. Contrairement à ce que suggère cette citation, il n'est pas clair que Schrödinger lui-même endosse le caractère rationaliste de cette position, qui n'est, je l'ai dit, pas la sienne. Il y a peut-être là une question de traduction. Je n'ai pas l'original en anglais, mais dans une traduction allemande (lien périmé) le mot correspondant est Verstandesmensch – qui signifie plutôt «esprit positif».
8. Florence Burgat avec la collaboration de Robert Dantzer, dir., Les animaux d'élevage ont-ils droit au bien-être?, Paris, INRA Éditions, 2001.
9. La conscience est accordée «par analogie» aussi aux «animaux les plus évolués». Dérogation bien fragile, on l'a vu, dans le cas par exemple des chercheurs de l'INRA; en fait, la conscience n'est pleinement accordée qu'aux humains.
10. On pourra se référer par exemple au chapitre 6 de l'ouvrage de Penrose, L'esprit, l'ordinateur et les lois de la physique, ou à Sven Ortoli et Jean-Pierre Pharabod, Le cantique des quantiques, éd. La Découverte.
11. Dans son célèbre pari, Pascal s'efforce de nous montrer que nous avons intérêt à croire en Dieu. Il se rend cependant compte que cela ne suffit pas; croire n'est pas un acte volontaire. Dès lors, il énumère des techniques permettant, en quelque sorte, de se laver soi-même le cerveau.
12. De façon générale, lorsque je dis «nous» dans cet article je ne parle pas spécifiquement des humains, mais de l'ensemble des êtres délibérants et sensibles.
13. Je mets des guillemets à ce terme, parce que dès lors qu'elles sont vraies, les assertions prescriptives peuvent aussi être vues comme des descriptions d'un état de fait.
14. Mathieu 14:25-31.
** Selon James Rachels dans “Moral Philosophy as a Subversive Activity” (Logos: A Journal of Catholic Thought and Culture 5, n°1 (1er février 2002)).
15. René Descartes, Discours de la méthode (1637), début de la troisième partie.
16. Descartes, encore (Discours de la méthode, troisième partie, un peu plus loin): «pour savoir quelles étaient véritablement leurs opinions, je devais plutôt prendre garde à ce qu'ils pratiquaient qu'à ce qu'ils disaient; non seulement à cause qu'en la corruption de nos mœurs il y a peu de gens qui veuillent dire tout ce qu'ils croient, mais aussi à cause que plusieurs l'ignorent eux-mêmes; car l'action de la pensée par laquelle on croit une chose étant différente de celle par laquelle on connaît qu'on la croit, elles sont souvent l'une sans l'autre.»
17. Il y a quelques années une amie devait subir un examen médical d'un genre parfois douloureux, justifiant une certaine forme d'anesthésie. Lors de la consultation préalable, l'anesthésiste lui expliqua qu'elle resterait consciente, mais qu'elle ne se souviendrait de rien par la suite; cette anesthésie ne supprimait peut-être pas la douleur, disait-il, mais puisqu'elle n'allait pas s'en souvenir, cela revenait au même. De son point de vue, donc, les sensations vécues non seulement par «les animaux du bas de l'échelle» (pour paraphraser le «rationaliste» de Schrödinger), mais aussi par une humaine en bonne et due forme relevaient de la «spéculation gratuite», dès lors que leur souvenir ne persistait pas (combien de temps?). Elles n'avaient pas de réalité par elles-mêmes, et les éviter ne devait pas constituer une fin, même pour la personne dont elles étaient les sensations futures. Le fait que ce discours puisse être tenu, et faire hésiter la personne elle-même, implique que la réalité d'un plaisir ou d'une souffrance futurs ne va pas toujours de soi, y compris pour la personne destinée à l'éprouver.
18. Pour une forme extrême, et quelque peu fascisante, de cette philosophie individualiste, voir par exemple l'Institut Ayn Rand.
19. Je ne crois pas en une telle existence, du moins en un sens fort: celle de l'individu comme tout indécomposable, perdurant de façon inaltérable au cours du temps. Je crois en l'existence de sensations, mais le «réceptacle» de ces sensations me semble beaucoup plus accidentel. Pour une discussion approfondie de la question de l'identité personnelle, voir Derek Parfit, Reasons and Persons, Oxford, 1992.
20. Les théories des droits ont pour une large part la même attitude, mais reconnaissent souvent aussi des «devoirs envers nous-mêmes». Ceux-ci ne consistent cependant généralement pas à se faire plaisir!
21. L'Institut Ayn Rand mentionné en note 19 énonce dans le résumé de sa philosophie (page «Essentials of Objectivism») le principe: «Ethics: Self-interest» («Notre éthique: l'intérêt égoïste»). Ses adeptes semblent tenir très fort à ce que tout le monde soit égoïste. Pour notre propre bien? On a envie de leur dire: mêlez-vous donc de ce qui vous regarde!
22. Le problème de la «faiblesse de la volonté» a reçu en philosophie le doux nom d'acrasie.
23. Cette expression, tout comme d'autres du même genre, était et est encore utilisée par les tenants de cette position; c'est certainement en écho à ces débats que Schrödinger la met dans la bouche de son «rationaliste».
24. J.M. Coetzee, The Lives of Animals, éd. Princeton University Press, p. 63 de l'édition paperback 2001.
25. Pierre-Simon de Laplace, Essai philosophique sur les probabilités, 1814, ch. «De la probabilité».
26. En fait, il suffit vraisemblablement de connaître cette valeur en une infinité dénombrable de points. Peu importe ce détail technique ici.
27. Selon Penrose (Les Ombres de l'esprit, section 1.3) il n'est pas clair que ce modèle classique, avec ses champs et donc un nombre infini de variables, soit réellement calculable, au sens défini plus loin (Penrose parle de «la physique d'aujourd'hui», mais cela revient au même, je pense, dans le contexte évoqué ici). Un tel éventuel caractère non calculable représenterait cependant une découverte, et ne fait donc pas partie du paradigme classique. Celui-ci reste bel et bien équivalent à un modèle «boules de billard».
28. Dans un célèbre discours tenu en 1900 («Nineteenth Century Clouds Over the Dynamic Theory of Heat and Light»), le physicien anglais Lord Kelvin affirmait que la physique était alors totalement achevée, à «deux petits nuages» près. On vit par la suite ce qu'il en était – un de ces petits nuages, en particulier, fut à l'origine de la première introduction des quanta, et donc lié à la naissance de la mécanique quantique et à l'écroulement que celle-ci impliqua de l'ensemble de l'édifice de la physique classique.
29. L'évolution du vecteur d'état est, en mécanique quantique, déterministe et réversible (à quelques nuances techniques près) tant que n'intervient pas de «mesure» du système; et c'est justement ce «principe de la mesure» qui possède un statut très particulier et empêche la mécanique quantique d'être une vraie théorie du monde physique. Par ailleurs, je laisse de côté le caractère irréversible des lois de la thermodynamique; car ces lois, qui sembleraient surdéterminer celles de la physique laplacienne, ne sont pas des lois d'évolution au sens où je l'entends ici. La thermodynamique est loin d'être sans rapport avec le sujet de cet article, mais l'aborder prendrait trop de place.
30. C'est un tel monde «laplacien-plus-plus» que supposait Descartes. Il croyait en l'existence d'un point précis dans le cerveau humain – point qu'il situait dans la glande pinéale – où l'âme entretenait une communication bidirectionnelle avec le corps. Chez les humains et eux seuls, donc, et en ce point seulement, l'ensemble des lois «mécaniques», déterministes, de la physique étaient rompues (informations tirées de Daniel Dennett, Consciousness Explained, éd. Little, Brown and Company, 1991, p. 34).
31. «Computing Machinery and Intelligence», 1950. L'article complet (en anglais) est disponible sur le site Web Abelard.
32. Fin de la section 5. En fait, l'interrogateur est confronté simultanément à un humain et à un ordinateur; il sait que l'un est humain et l'autre machine, mais il ne sait pas lequel. Le jeu consiste à tenter de le déterminer.
33. En toute rigueur, cela implique que les animaux non humains ne peuvent pas penser, ainsi que beaucoup d'humains, comme je l'indique plus loin. Turing affirme pourtant dans le même article, en substance, que les animaux non humains ressemblent plus aux humains qu'aux cailloux. C'est déjà une position rare!
34. La température n'est plus définie aujourd'hui comme dans l'exemple que j'ai cité. La thermodynamique n'en reste cependant pas moins un domaine de prédilection pour les attitudes opérationaliste; peut-être parce que les concepts fondamentaux de thermodynamique, y compris celui de température, impliquent un recours à des notions de probabilité et/ou de contrefactualité, c'est-à-dire ne peuvent pas être définis dans le cadre même de la physique laplacienne.
35. Section 6, objection 4.
36. Section 2.
37. L'esprit, l'ordinateur et les lois de la physique, chapitre 10, par exemple; et Les Ombres de l'esprit, section 1.9.
38. Aux réserves près que fait Penrose dans Les Ombres de l'esprit, section 1.3.
39. Pour une définition précise, voir L'esprit, l'ordinateur et les lois de la physique, chapitre 2.
40. Exemple de pavage tiré des Ombres de l'esprit, section 1.9.
41. Les Ombres de l'esprit, chapitre 7.
42. L'esprit, l'ordinateur et les lois de la physique, chapitre 10, section 15.
43. À vrai dire, dans le cadre de la théorie de la relativité (depuis 1905, donc), le point de vue «monde historique» est le seul légitime; c'est le monde instantané qui est réduit à l'état de fiction, puisque la notion de «même instant» en des lieux différents de l'univers n'a plus de sens. Cela ne change pas le fond de mon exposé, où la notion de monde instantané sert surtout à introduire celle de monde historique.
44. Pour des raisons certainement historiques, cette expression a une certaine connotation religieuse. Je l'utiliserai cependant à l'occasion, sans y accorder de signification religieuse, parce qu'elle est plus spécifique que le simple mot «liberté».
45. La pratique des tribunaux, tout comme les traditions religieuses, associent à la notion de liberté celles de culpabilité et de mérite. Je ne crois pas en la réalité de ces notions-là.
46. En fait, la causalité n'implique pas toujours un rapport de nécessité, ni un rapport de suffisance. Il n'est pas nécessaire qu'Élodie jette le caillou pour qu'il tombe sur la chaussée (Sofia aurait pu le faire à sa place); il n'est pas non plus suffisant qu'elle le fasse (un fort vent pourrait dévier le caillou, le faisant tomber sur le gazon). Je laisse de côté ces complications.
47. Je remercie Estiva de m'avoir signalé ce paradoxe; bien qu'elle ne soit pas en accord avec ma conclusion!
48. Sur les mondes multiples, une bonne introduction (en anglais) se trouve sur le site Web http://www.hedweb.com/everett/.
49. Les Ombres de l'esprit, chapitre 7.
50. René Descartes, Discours de la Méthode, début de la quatrième partie.
51. Descartes: «mon opinion est moins cruelle envers les bêtes qu'elle n'est pieuse envers les hommes qui sont asservis à la superstition des Pythagoriciens [qui étaient végétaliens] et qui sont délivrés du soupçon du crime toutes les fois qu'ils mangent ou tuent des animaux» (Lettre à Morus, 5 février 1649, extrait cité sur le site Web http://rdereel.free.fr/).
52. On pourrait encore imaginer qu'elle ne dépende pas de mon plaisir et de ma souffrance à moi, mais seulement de ceux d'autrui. Je laisse de côté cette hypothèse peu plausible et dont l'examen ne modifierait pas, je crois, ma conclusion.
53. La respiration est chez l'être humain un acte semi-automatique. Nous respirons souvent sans l'avoir décidé; ce que j'affirme ici vaut dès lors que nous nous posons la question.
54. Les Ombres de l'esprit, chapitre 2.
55. Voir Alan Turing, «Computing Machinery and Intelligence», section 6, objection 3.
56. Les Ombres de l'esprit, section 3.4.
57. Voir l'ensemble du chapitre 3 pour une discussion détaillée.
58. L'esprit, l'ordinateur et les lois de la physique, section 10.7; Les Ombres de l'esprit, section 8.6.
59. L'esprit, l'ordinateur et les lois de la physique, section 1.5.
60. Voir Estiva Reus, «Lectures de pensée animale», page 142 du numéro 23 des Cahiers.
61. «Effet» n'est pas vraiment le bon terme, ici, puisqu'il suggère un caractère épiphénoménal des sensations; de même qu'il faudrait dire, non que l'exécution induit la sensation, mais qu'elle est la sensation, ou qu'elle la contient. Je continuerai à utiliser le langage habituel, par simplicité.
62. Les Ombres de l'esprit, section 1.3.
